Advertisements
Advertisements
प्रश्न
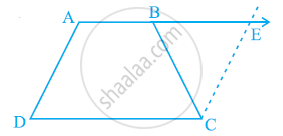
ABCD एक समलंब है, जिसमें AB || DC और AD = BC है (देखिए आकृति में)। दर्शाइए कि
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- विकर्ण AC = विकर्ण BD है।
[संकेत: AB को बढ़ाइए और C से होकर DA के समांतर एक रेखा खींचिए जो बढ़ी हुई भुजा AB को E पर प्रतिच्छेद करे।]
उत्तर
हमें एक समलंब चतुर्भुज ABCD दिया गया है जिसमें AB || CD तथा AD = BC है।
(i) AB को E तक बढाकर CE || AD खींचिए ...(1)
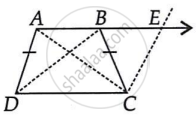
∵ AB || DC ⇒ AE || DC
साथ ही, AD || CE ...[(1) से]
∴ AECD एक समांतर चतुर्भुज है।
⇒ AD = CE ...(1) ...[∵ समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।]
लेकिन AD = BC ...(2) ...[दिया गया है।]
(1) और (2) से, BC = CE
अब, ΔBCE में, BC = CE है
⇒ ∠CEB = ∠CBE ...(3) ...[∵ त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।]
साथ ही, ∠ABC + ∠CBE = 180° ...(4) ...[रैखिक युग्म]
और ∠A + ∠CEB = 180° ...(5) ...[समांतर चतुर्भुज ADCE के सह-आंतरिक कोण]
(4) और (5) से, हमें प्राप्त होता है
∠ABC + ∠CBE = ∠A + ∠CEB
⇒ ∠ABC = ∠A ...[(3) से]
⇒ ∠B = ∠A ...(6)
(ii) AB || CD तथा AD एक तिर्यक रेखा है।
∴ ∠A + ∠D = 180° ...(7) ...[सह-आंतरिक कोण]
इसी प्रकार, ∠B + ∠C = 180° ...(8)
(7) और (8) से, हमें प्राप्त होता है
∠A + ∠D = ∠B + ∠C
⇒ ∠C = ∠D ...[(6) से]
(iii) ΔABC और ΔBAD में, हमारे पास है
AB = BA ...[उभयनिष्ठ]
BC = AD ...[दिया गया है।]
∠ABC = ∠BAD ...[सिद्ध हुआ।]
∴ ΔABC ≅ ΔBAD ...[SAS सर्वांगसमता से]
(iv) चूँकि, ΔABC ≅ ΔBAD ...[सिद्ध हुआ।]
⇒ AC = BD ...[C.P.C.T. से]
APPEARS IN
संबंधित प्रश्न
समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति में)। दर्शाइए कि
- यह ∠C को भी समद्विभाजित करता है।
- ABCD एक समचतुर्भुज है

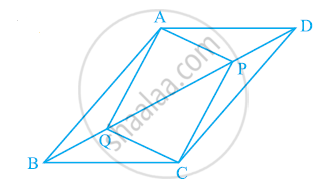
समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP = BQ है (देखिए आकृति में)। दर्शाइए कि
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ एक समांतर चतुर्भुज है।
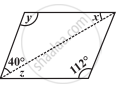
निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए :

निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि AB = DC = 8 cm, AD = 4 cm और BC = 4.4 cm?
एक चतुर्भुज का नाम बताइए जिसके विकर्ण एक दूसरे को समद्विभाजित करते है।
एक चतुर्भुज ABCD के सम्मुख कोण बराबर हैं। यदि AB = 4 cm है, तो CD निर्धारित कीजिए।
एक समांतर चतुर्भुज ABCD में, AB = 10 cm और AD = 6 cm है। ∠A का समद्विभाजक DC से E पर मिलता है तथा AE और BC बढ़ाने पर F पर मिलते हैं। CF की लंबाई ज्ञात कीजिए।
नीचे दी गयी आकृति में, ABCD और BDCE एक ही आधार DC पर दो समांतर चतुर्भुज हैं। यदि BC ⊥ BD है, तो ∠BEC बराबर है –
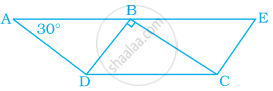
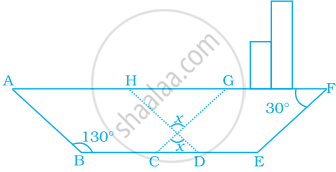
नीचे दिये गये एक जहाज कौँ आकृति में, ABDH और CEFG दो समांतर चतुर्भुज हैं। x का मान ज्ञात कीजिए।