Advertisements
Advertisements
प्रश्न
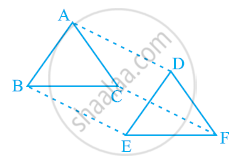
ΔABC और ΔDEF में, AB = DE, AB || DE, BC = EF और BC || EF है | शीर्षों A, B और C को क्रमश: शीर्षों D, E और F से जोड़ा जाता है | दर्शाइए कि
- चतुर्भुज ABED एक समांतर चतुर्भुज है।
- चतुर्भुज BEFC एक समांतर चतुर्भुज है।
- AD || CF और AD = CF है |
- चतुर्भुज ACFD एक समांतर चतुर्भुज है।
- AC = DF है
- Δ ABC ≅ Δ DEF है
उत्तर
(i) चतुर्भुज ABED में
AB = DE और AB || DF दिया है |
∴ चतुर्भुज ABED एक समांतर चतुर्भुज है |
( यदि किसी चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर और समांतर हो तो वह समांतर चतुर्भुज होता है )
अब, चूँकि ABED एक समांतर चतुर्भुज है |
∴ AD = BE और AD|| BE .........(1)
(समांतर चतुर्भुज की सम्मुख भुजा बराबर और समांतर होती है)
(ii) इसीप्रकार से, चतुर्भुज BEFC में
BC = EF और BC||EF दिया है |
∴चतुर्भुज BEFC एक समांतर चतुर्भुज है |
अत: CF = BE और CF||BE ........... (2) (समांतर चतुर्भुज की सम्मुख)
(iii) समीo (1) तथा (2) से
AD || CF और AD = CF है|
(चूँकि सम्मुख भुजाओं का एक युग्म बराबर और समांतर है)
∴चतुर्भुज ACFD एक समांतर चतुर्भुज है।
इसलिए, AC = DF और AC||DF .......... (3)
(vi) Δ ABC और Δ DEF में,
AB = DE (दिया है)
BC = EF (दिया है)
AC = DF (समीo 3 से)
S.S.S सर्वांगसमता नियम से
∴ ΔABC ≅ ΔDEF
