Advertisements
Advertisements
प्रश्न
एक समांतर चतुर्भुज ABCD में, AB = 10 cm और AD = 6 cm है। ∠A का समद्विभाजक DC से E पर मिलता है तथा AE और BC बढ़ाने पर F पर मिलते हैं। CF की लंबाई ज्ञात कीजिए।
उत्तर
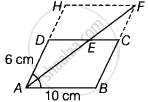
दिया गया है, AB = 10 cm, AD = 6 cm
DC = AB = 10 cm और AD = BC = 6 cm
दिया गया है, ∠A का समद्विभाजक DE को E पर और BC को F पर बढ़ाता है।
अब, PF || CD निकालना।
आकृति से,
CD || FP और CF || DP
PDCF एक समानांतर चतुर्भुज है।
और AB || FP और AP || BF
ABFP भी एक समांतर चतुर्भुज है।
ΔAPF और ΔABF में,
∠APF = ∠ABF ...(समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।)
AF = AF ...(उभयनिष्ठ पक्ष)
∠PAF = ∠AFB ...(वैकल्पिक कोण)
ΔAPF ≅ ΔABF ...(ASA सर्वांगसमता कसौटी के अनुसार)
AB = AP ...(CPCT)
AB = AD + DP
= AD + CF ...(क्योंकि DCFP एक समांतर चतुर्भुज है।)
∴ CF = AB – AD
= (10 – 6) cm
= 4 cm
APPEARS IN
संबंधित प्रश्न
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति में)। दर्शाइए कि
- यह ∠C को भी समद्विभाजित करता है।
- ABCD एक समचतुर्भुज है

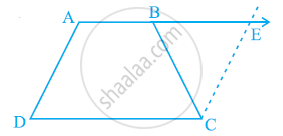
ABCD एक समलंब है, जिसमें AB || DC और AD = BC है (देखिए आकृति में)। दर्शाइए कि
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- विकर्ण AC = विकर्ण BD है।
[संकेत: AB को बढ़ाइए और C से होकर DA के समांतर एक रेखा खींचिए जो बढ़ी हुई भुजा AB को E पर प्रतिच्छेद करे।]
किसी समांतर चतुर्भुज के दो आसन्न कोनो के माप बराबर हैं। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
एक चतुर्भुज का नाम बताइए जिसके विकर्ण एक दूसरे को समद्विभाजित करते है।
एक समांतर चतुर्भुज के विकर्ण परस्पर लंब होते हैं। क्या यह कथन सत्य है? अपने उत्तर के लिए कारण दीजिए।
यदि एक चतुर्भुज के सम्मुख कोण बराबर हों, तो वह अवश्य ही समांतर चतुर्भुज होगा।
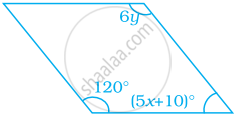
निम्न समांतर चतुर्भुज में, x और y के मान ज्ञात कीजिए –
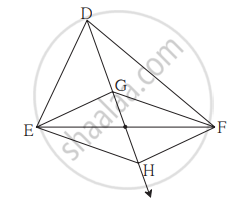
आकृति में, बिंदु G, ΔDEF की माध्यिकाओं का संगामी बिंदु है। किरण DG पर बिंदु H इस प्रकार लें कि D-G-H तथा DG = GH, हो तो सिद्ध कीजिए कि `square` GEHF समांतर चतुर्भुज है।
संलग्न आकृति में समांतर चतुर्भुज `square` ABCD की भुजाओं पर P, Q, R, S इस प्रकार है कि, AP = BQ = CR = DS तो सिद्ध कीजिए कि `square` PQRS समांतर चतुर्भुज है।

