Advertisements
Advertisements
प्रश्न
एक समांतर चतुर्भुज ABCD में, AB = 10 cm और AD = 6 cm है। ∠A का समद्विभाजक DC से E पर मिलता है तथा AE और BC बढ़ाने पर F पर मिलते हैं। CF की लंबाई ज्ञात कीजिए।
उत्तर
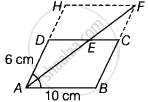
दिया गया है, AB = 10 cm, AD = 6 cm
DC = AB = 10 cm और AD = BC = 6 cm
दिया गया है, ∠A का समद्विभाजक DE को E पर और BC को F पर बढ़ाता है।
अब, PF || CD निकालना।
आकृति से,
CD || FP और CF || DP
PDCF एक समानांतर चतुर्भुज है।
और AB || FP और AP || BF
ABFP भी एक समांतर चतुर्भुज है।
ΔAPF और ΔABF में,
∠APF = ∠ABF ...(समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।)
AF = AF ...(उभयनिष्ठ पक्ष)
∠PAF = ∠AFB ...(वैकल्पिक कोण)
ΔAPF ≅ ΔABF ...(ASA सर्वांगसमता कसौटी के अनुसार)
AB = AP ...(CPCT)
AB = AD + DP
= AD + CF ...(क्योंकि DCFP एक समांतर चतुर्भुज है।)
∴ CF = AB – AD
= (10 – 6) cm
= 4 cm
APPEARS IN
संबंधित प्रश्न
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
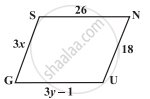
निम्न आकृति GUNS समांतर चतुर्भुज हैं। x तथा y ज्ञात कीजिए (लंबाई cm में है) :
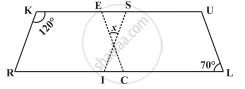
दी गई आकृति में RISK तथा CLUE दोनों समांतर चतुर्भुज हैं, x का मान ज्ञात कीजिए।
एक समांतर चतुर्भुज के विकर्ण परस्पर लंब होते हैं। क्या यह कथन सत्य है? अपने उत्तर के लिए कारण दीजिए।
चतुर्भुज ABCD में, ∠A + ∠D = 180° है। इस चतुर्भुज को कौन-सा विशेष नाम दिया जा सकता है?
निम्नलिखित आकृति में, यह दिया है कि BDEF और FDCE समांतर चतुर्भुज हैं। क्या आप कह सकते हैं कि BD = CD है? क्यों और क्यों नहीं?

ABCD एक समचतुर्भुज है, जिसमें D से AB पर शीर्षलंब AB को समद्विभाजित करता है। समचतुर्भुज के कोण ज्ञात कीजिए।
आकृति में `square` ABCD समांतर चतुर्भुज है। किरण AB पर बिंदु E इस प्रकार है कि BE = AB तो सिद्ध कीजिए कि रेखा ED यह रेख BC को बिंदु F पर समद्विभाजित करती है।

समांतर चतुर्भुज की दो संलग्न भुजाओं का अनुपात 3 : 4 है। उसकी परिमिति 112 सेमी हो तो उसकी प्रत्येक भुजा की लंबाई ज्ञात कीजिए।
संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR