Advertisements
Advertisements
प्रश्न
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
उत्तर
मान लीजिए ABCD एक वर्ग है जिसके विकर्ण AC और BD एक दूसरे को बिंदु O पर प्रतिच्छेद करते हैं।
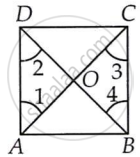
(i) यह सिद्ध करने के लिए कि विकर्ण बराबर हैं, हमें AC = BD सिद्ध करना होगा।
ΔABC और ΔBAD में, हमारे पास है
AB = BA ...[उभयनिष्ठ]
BC = AD ...[वर्ग ABCD की भुजाएँ]
∠ABC = ∠BAD ...[प्रत्येक कोण 90° है]
∴ ΔABC ≅ ΔBAD ...[SAS सर्वांगसमता से]
⇒ AC = BD ...[CPCT से] ...(1)
(ii) AD || BC और AC एक तिर्यक रेखा है। ...[∵ वर्ग एक समांतर चतुर्भुज है।]
∴ ∠1 = ∠3 ...[एकांतर अंतः कोण बराबर हैं।]
इसी प्रकार, ∠2 = ∠4
अब, ΔOAD और ΔOCB में, हमारे पास है
AD = CB ...[वर्ग ABCD की भुजाएँ]
∠1 = ∠3 ...[सिद्ध हुआ।]
∠2 = ∠4 ...[सिद्ध हुआ।]
∴ ΔOAD ≅ ΔOCB ...[ASA सर्वांगसमता से]
⇒ OA = OC और OD = OB ...[CPCT से] ...(2)
अर्थात् विकर्ण AC और BD एक दूसरे को बिंदु O पर समद्विभाजित करते हैं।
(iii) ΔOBA और ΔODA में, हमारे पास है
OB = OD ...[सिद्ध हुआ।]
BA = DA ...[वर्ग ABCD की भुजाएँ]
OA = OA ...[उभयनिष्ठ]
∴ ΔOBA ≅ ΔODA ...[SSS सर्वांगसमता से]
⇒ ∠AOB = ∠AOD ...[CPCT से] ... (3)
∵ ∠AOB और ∠AOD एक रैखिक युग्म बनाते हैं।
∴ ∠AOB + ∠AOD = 180°
∴ ∠AOB = ∠AOD = 90° ...[(3) से]
⇒ AC ⊥ BD ...(4)
(1), (2) और (4) से हम पाते हैं कि AC और BD बराबर हैं और एक दूसरे को समकोण पर समद्विभाजित करते हैं।
APPEARS IN
संबंधित प्रश्न
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠A = 70° और ∠C = 65°?
∆ABC में, AB = 5 cm, BC = 8 cm और CA = 7 cm हैं। यदि D और E क्रमश : AB और BC के मध्य-बिंदु हैं, तो DE की लंबाई निर्धारित कीजिए।
एक चतुर्भुज ABCD के सम्मुख कोण बराबर हैं। यदि AB = 4 cm है, तो CD निर्धारित कीजिए।
ABCD एक समचतुर्भुज है, जिसमें D से AB पर शीर्षलंब AB को समद्विभाजित करता है। समचतुर्भुज के कोण ज्ञात कीजिए।
E एक समलंब ABCD की भुजा AD का मध्य-बिंदु है, जिसमें AB || DC है। E से होकर AB के समांतर खींची गई रेखा BC को F पर प्रतिच्छेद करती है। दर्शाइए कि F भुजा BC का मध्य-बिंदु है। [संकेत : AC को मिलाइए]
किसी समांतर चतुर्भुज के एक अधिक कोण वाले शीर्ष से खींचे गये दो शीर्षलंबों के बीच का कोण 30∘ है। उस अधिक कोण की माप है –
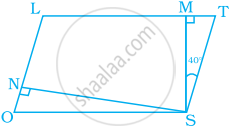
समांतर चतुर्भुज LOST में, SN ⊥ OL और SM ⊥ LT है। ∠STM, ∠SON और ∠NSM ज्ञात कीजिए।
किसी चतुर्भुज के दो कोणों में से प्रत्येक की माप 75∘ है तथा अन्य दो कोण बराबर हैं। इन दोनों कोणों के माप क्या हैं? संभावित बनने वाली आकृतियों के नाम लिखिए।
समांतर ABCD में, ∠A का समद्विभाजक BC को समद्विभाजित करता है। क्या कोण B का समद्विभाजक AD को भी समद्विभाजित करता है? कारण दीजिए।
समांतर चतुर्भुज की दो संलग्न भुजाओं का अनुपात 3 : 4 है। उसकी परिमिति 112 सेमी हो तो उसकी प्रत्येक भुजा की लंबाई ज्ञात कीजिए।
