Advertisements
Advertisements
प्रश्न
समांतर चतुर्भुज की दो संलग्न भुजाओं का अनुपात 3 : 4 है। उसकी परिमिति 112 सेमी हो तो उसकी प्रत्येक भुजा की लंबाई ज्ञात कीजिए।
उत्तर
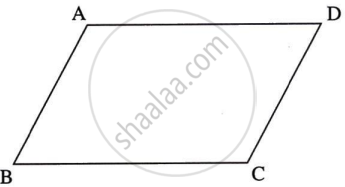
मानो `square` ABCD समांतर चतुर्भुज है।
AB : BC = 3 : 4
यदि AB = 3x सेमी
तो, BC = 4x सेमी ...(x सामान्य गुणज है।)
∴ CD = AB = 3x सेमी
तथा AD = BC = 4x सेमी ...(समांतर चतुर्भुज की सम्मुख भुजाएँ)
`square` ABCD की परिमिति = 112 सेमी
∴ AB + BC + CD + AD = 112
∴ 3x + 4x + 3x + 4x = 112
∴ 14x = 112
∴ x =`112/14`
∴ x = 8
∴ CD = AB = 3x = 3 × 8 = 24 सेमी
∴ AD = BC = 4x = 4 × 8 = 32 सेमी
APPEARS IN
संबंधित प्रश्न
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
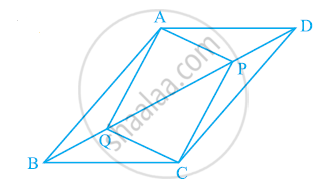
समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP = BQ है (देखिए आकृति में)। दर्शाइए कि
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ एक समांतर चतुर्भुज है।
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠D +∠B = 180°?
किसी समांतर चतुर्भुज के दो आसन्न कोणों का अनुपात 3 : 2 है। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
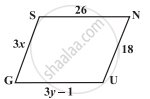
निम्न आकृति GUNS समांतर चतुर्भुज हैं। x तथा y ज्ञात कीजिए (लंबाई cm में है) :
एक चतुर्भुज का नाम बताइए जिसके विकर्ण एक दूसरे को समद्विभाजित करते है।
यदि किसी समांतर चतुर्भुज के दो आसन्न कोण (5x − 5)∘ और (10x + 35)∘ हैं, तो इन कोणों का अनुपात होगा –
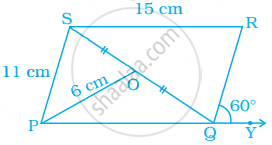
नीचे दिये समांतर चतुर्भुज PQRS में, O विकर्ण SQ का मध्य बिंदु है। ∠S, ∠R, PQ, QR और विकर्ण PR ज्ञात कीजिए।
एक समांतर चतुर्भुज की रचना कीजिए जिसकी एक भुजा 4 cm और दोनों विकर्ण 5.6 cm और 7 cm हों। दूसरी भुजा को मापिए।
संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR