Advertisements
Advertisements
प्रश्न
समांतर चतुर्भुज की दो संलग्न भुजाओं का अनुपात 3 : 4 है। उसकी परिमिति 112 सेमी हो तो उसकी प्रत्येक भुजा की लंबाई ज्ञात कीजिए।
उत्तर
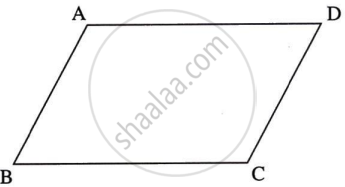
मानो `square` ABCD समांतर चतुर्भुज है।
AB : BC = 3 : 4
यदि AB = 3x सेमी
तो, BC = 4x सेमी ...(x सामान्य गुणज है।)
∴ CD = AB = 3x सेमी
तथा AD = BC = 4x सेमी ...(समांतर चतुर्भुज की सम्मुख भुजाएँ)
`square` ABCD की परिमिति = 112 सेमी
∴ AB + BC + CD + AD = 112
∴ 3x + 4x + 3x + 4x = 112
∴ 14x = 112
∴ x =`112/14`
∴ x = 8
∴ CD = AB = 3x = 3 × 8 = 24 सेमी
∴ AD = BC = 4x = 4 × 8 = 32 सेमी
APPEARS IN
संबंधित प्रश्न
समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति में)। दर्शाइए कि
- यह ∠C को भी समद्विभाजित करता है।
- ABCD एक समचतुर्भुज है

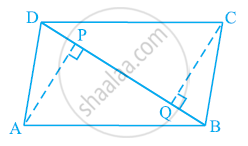
ABCD एक समांतर चतुर्भज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं (देखिए आकृति में)। दर्शाइए कि
- ΔAPB ≅ ΔCQD
- AP = CQ
निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:

क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠D +∠B = 180°?
E एक समलंब ABCD की भुजा AD का मध्य-बिंदु है, जिसमें AB || DC है। E से होकर AB के समांतर खींची गई रेखा BC को F पर प्रतिच्छेद करती है। दर्शाइए कि F भुजा BC का मध्य-बिंदु है। [संकेत : AC को मिलाइए]
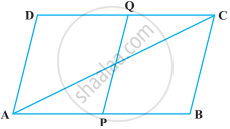
एक समांतर चतुर्भुज ABCD की सम्मुख भुजाओं AB और CD पर क्रमश : बिंदु P और Q इस प्रकार लिए गए हैं कि AP = CQ है। (आकृति)। दर्शाइए कि AC और PQ परस्पर समद्विभाजित करते हैं।
एक समांतर चतुर्भुज ABCD में, AB = 10 cm और AD = 6 cm है। ∠A का समद्विभाजक DC से E पर मिलता है तथा AE और BC बढ़ाने पर F पर मिलते हैं। CF की लंबाई ज्ञात कीजिए।
सभी आयत समांतर चतुर्भुज होते हैं।
ABCD एक समांतर चतुर्भुज है। भुजा AB और AD पर क्रमशः बिंदु P और Q इस प्रकार लिये गये हैं कि एक समांतर चतुर्भुज PRQA बनता है। यदि ∠C = 45∘ है, तो ∠R ज्ञात कीजिए।
संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR