Advertisements
Advertisements
प्रश्न
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠D +∠B = 180°?
उत्तर
सम्मुख कोणों का योग 180° होना चाहिए।
आसन्न कोणों का माप भी समान होना चाहिए।
APPEARS IN
संबंधित प्रश्न
यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि:
- ABCD एक वर्ग है।
- विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
बताइए कैसे एक वर्ग एक समांतर चतुर्भुज है।
निम्नलिखित के लिए कारण दीजिए:
वर्ग, आयत, समांतर चतुर्भुज और समचतुर्भुज में से प्रत्येक एक चतुर्भुज भी है।
एक चतुर्भुज ABCD के विकर्ण परस्पर समद्विभाजित करते हैं। यदि ∠A = 35° है, तो ∠B निर्धारित कीजिए।
एक चतुर्भुज ABCD के सम्मुख कोण बराबर हैं। यदि AB = 4 cm है, तो CD निर्धारित कीजिए।
ABCD एक समलंब है जिसमें AB || DC और ∠A = ∠B = 45° है। इस समलंब के कोण C और D ज्ञात कीजिए।
E एक समलंब ABCD की भुजा AD का मध्य-बिंदु है, जिसमें AB || DC है। E से होकर AB के समांतर खींची गई रेखा BC को F पर प्रतिच्छेद करती है। दर्शाइए कि F भुजा BC का मध्य-बिंदु है। [संकेत : AC को मिलाइए]
सभी आयत समांतर चतुर्भुज होते हैं।
यदि एक चतुर्भुज के सम्मुख कोण बराबर हों, तो वह अवश्य ही समांतर चतुर्भुज होगा।
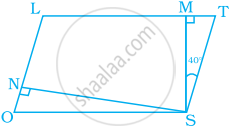
समांतर चतुर्भुज LOST में, SN ⊥ OL और SM ⊥ LT है। ∠STM, ∠SON और ∠NSM ज्ञात कीजिए।
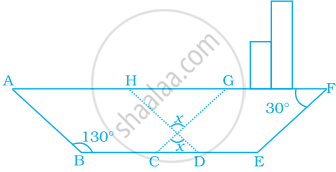
नीचे दिये गये एक जहाज कौँ आकृति में, ABDH और CEFG दो समांतर चतुर्भुज हैं। x का मान ज्ञात कीजिए।
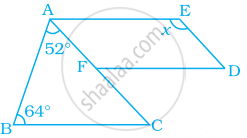
निम्न आकृति में, FD || BC || AE है और AC || ED है। x का मान ज्ञात कीजिए –
एक समांतर चतुर्भुज ABCD की रचना कीजिए, जिसमें AB = 4cm, BC = 5 cm और ∠B = 60∘ है।
आकृति में `square` PQRS तथा `square` ABCR दो समांतर चतुर्भुज है। ∠P = 110° तो `square `ABCR के सभी कोणों के माप ज्ञात कीजिए।

संलग्न आकृति में समांतर चतुर्भुज `square` ABCD की भुजाओं पर P, Q, R, S इस प्रकार है कि, AP = BQ = CR = DS तो सिद्ध कीजिए कि `square` PQRS समांतर चतुर्भुज है।

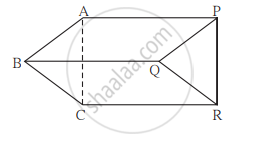
संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR