Advertisements
Advertisements
प्रश्न
यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
उत्तर
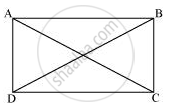
मान लीजिए ABCD एक समांतर चतुर्भुज है। यह दर्शाने के लिए कि ABCD एक आयत है, हमें यह सिद्ध करना होगा कि इसका एक अंत: कोण 90° है।
ΔABC और ΔDCB में,
AB = DC ...(समानांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।)
BC = BC ...(उभयनिष्ठ)
AC = DB ...(दिया गया है।)
∴ ΔABC ≅ ΔDCB ...(SSS सर्वांगसमता नियम से)
⇒ ∠ABC = ∠DCB
यह ज्ञात है कि तिर्यक रेखा के एक ही ओर के कोणों के मापों का योग 180º होता है।
∠ABC + ∠DCB = 180° ...(AB || CD)
⇒ ∠ABC + ∠ABC = 180°
⇒ 2∠ABC = 180°
⇒ ∠ABC = 90°
क्योंकि ABCD एक समांतर चतुर्भुज है और इसका एक अंत: कोण 90° है, इसलिए ABCD एक आयत है।
APPEARS IN
संबंधित प्रश्न
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠A = 70° और ∠C = 65°?
चतुर्भुज ABCD में, ∠A + ∠D = 180° है। इस चतुर्भुज को कौन-सा विशेष नाम दिया जा सकता है?
एक समांतर चतुर्भुज के एक अधिक कोण के शीर्ष से खींचे गए उस समांतर चतुर्भुज के दो शीर्षलंबों के बीच का कोण 60° है। इस समांतर चतुर्भुज के सभी कोण ज्ञात कीजिए।
निम्न में से कौन एक समांतर चतुर्भुज का गुण है?
समांतर चतुर्भुज LOST में, SN ⊥ OL और SM ⊥ LT है। ∠STM, ∠SON और ∠NSM ज्ञात कीजिए।
ABCD एक समांतर चतुर्भुज है। कोण A का समद्विभाजक CD को X पर प्रतिच्छेद करता है तथा कोण C का समद्विभाजक AB को Y पर प्रतिच्छेद करता है। क्या AXCY एक समांतर चतुर्भुज है? कारण दीजिए।
सिद्ध कीजिए कि एक समांतर चतुर्भुज के कोणों के समद्विभाजकों द्वारा बना चतुर्भुज एक आयत होता है।
आकृति में, बिंदु G, ΔDEF की माध्यिकाओं का संगामी बिंदु है। किरण DG पर बिंदु H इस प्रकार लें कि D-G-H तथा DG = GH, हो तो सिद्ध कीजिए कि `square` GEHF समांतर चतुर्भुज है।
संलग्न आकृति में समांतर चतुर्भुज `square` ABCD की भुजाओं पर P, Q, R, S इस प्रकार है कि, AP = BQ = CR = DS तो सिद्ध कीजिए कि `square` PQRS समांतर चतुर्भुज है।

संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR