Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि एक समांतर चतुर्भुज के कोणों के समद्विभाजकों द्वारा बना चतुर्भुज एक आयत होता है।
उत्तर
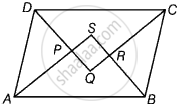
दिया गया है - मान लीजिए ABCD एक समांतर चतुर्भुज है और AP, BR, CR क्रमश : ∠A, ∠B, ∠C और ∠D के समद्विभाजक हैं।
सिद्ध करना है - चतुर्भुज PQRS एक आयत है।
उपपत्ति - चूँकि, ABCD एक समांतर चतुर्भुज है, तो DC || AB और DA एक तिर्यक रेखा है।
∠A + ∠D = 180° ...[एक समांतर चतुर्भुज के अंतः कोणों का योग 180° है।]
⇒ `1/2` ∠A + `1/2` ∠D = 90° ...[दोनों पक्षों को 2 से विभाजित करने पर]
∠PAD + ∠PDA = 90°
∠APD = 90° ...[चूँकि, त्रिभुज के सभी कोणों का योग 180° होता है।]
∴ ∠SPQ = 90° ...[शीर्षाभिमुख कोण]
∠PQR = 90°
∠QRS = 90°
और ∠PSR = 90°
इस प्रकार, PQRS एक चतुर्भुज है जिसका प्रत्येक कोण 90° है।
अतः, PQRS एक आयत है।
APPEARS IN
संबंधित प्रश्न
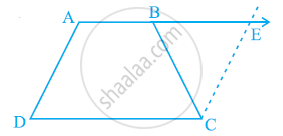
ABCD एक समलंब है, जिसमें AB || DC और AD = BC है (देखिए आकृति में)। दर्शाइए कि
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- विकर्ण AC = विकर्ण BD है।
[संकेत: AB को बढ़ाइए और C से होकर DA के समांतर एक रेखा खींचिए जो बढ़ी हुई भुजा AB को E पर प्रतिच्छेद करे।]
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠A = 70° और ∠C = 65°?
एक चतुर्भुज की कच्ची आकृति खीचिए जो समांतर चतुर्भुज न हो परंतु जिसके दो सम्मुख कोणों के माप बराबर हों।
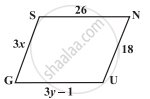
निम्न आकृति GUNS समांतर चतुर्भुज हैं। x तथा y ज्ञात कीजिए (लंबाई cm में है) :
एक चतुर्भुज ABCD के विकर्ण परस्पर समद्विभाजित करते हैं। यदि ∠A = 35° है, तो ∠B निर्धारित कीजिए।
यदि किसी समांतर चतुर्भुज के दो आसन्न कोण (5x − 5)∘ और (10x + 35)∘ हैं, तो इन कोणों का अनुपात होगा –
ABCD एक समांतर चतुर्भुज है। भुजा AB और AD पर क्रमशः बिंदु P और Q इस प्रकार लिये गये हैं कि एक समांतर चतुर्भुज PRQA बनता है। यदि ∠C = 45∘ है, तो ∠R ज्ञात कीजिए।
समांतर ABCD में, ∠A का समद्विभाजक BC को समद्विभाजित करता है। क्या कोण B का समद्विभाजक AD को भी समद्विभाजित करता है? कारण दीजिए।
किसी समांतर चतुर्भुज के दो संलग्न कोणों के मापों का अनुपात 1 : 2 हो तो उस समांतर चतुर्भुज के सभी कोणों के माप ज्ञात कीजिए।
आकृति में `square` ABCD समांतर चतुर्भुज है। किरण AB पर बिंदु E इस प्रकार है कि BE = AB तो सिद्ध कीजिए कि रेखा ED यह रेख BC को बिंदु F पर समद्विभाजित करती है।

