Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि एक समांतर चतुर्भुज के कोणों के समद्विभाजकों द्वारा बना चतुर्भुज एक आयत होता है।
उत्तर
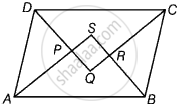
दिया गया है - मान लीजिए ABCD एक समांतर चतुर्भुज है और AP, BR, CR क्रमश : ∠A, ∠B, ∠C और ∠D के समद्विभाजक हैं।
सिद्ध करना है - चतुर्भुज PQRS एक आयत है।
उपपत्ति - चूँकि, ABCD एक समांतर चतुर्भुज है, तो DC || AB और DA एक तिर्यक रेखा है।
∠A + ∠D = 180° ...[एक समांतर चतुर्भुज के अंतः कोणों का योग 180° है।]
⇒ `1/2` ∠A + `1/2` ∠D = 90° ...[दोनों पक्षों को 2 से विभाजित करने पर]
∠PAD + ∠PDA = 90°
∠APD = 90° ...[चूँकि, त्रिभुज के सभी कोणों का योग 180° होता है।]
∴ ∠SPQ = 90° ...[शीर्षाभिमुख कोण]
∠PQR = 90°
∠QRS = 90°
और ∠PSR = 90°
इस प्रकार, PQRS एक चतुर्भुज है जिसका प्रत्येक कोण 90° है।
अतः, PQRS एक आयत है।
APPEARS IN
संबंधित प्रश्न
समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति में)। दर्शाइए कि
- यह ∠C को भी समद्विभाजित करता है।
- ABCD एक समचतुर्भुज है

निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:
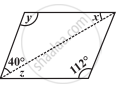
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि AB = DC = 8 cm, AD = 4 cm और BC = 4.4 cm?
किसी समांतर चतुर्भुज के दो आसन्न कोनो के माप बराबर हैं। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
दी गई आकृति में RISK तथा CLUE दोनों समांतर चतुर्भुज हैं, x का मान ज्ञात कीजिए।
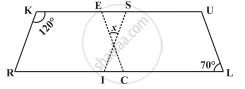
एक चतुर्भुज का नाम बताइए जिसके विकर्ण एक दूसरे को समद्विभाजित करते है।
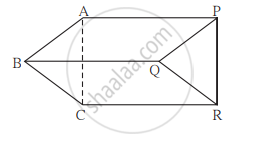
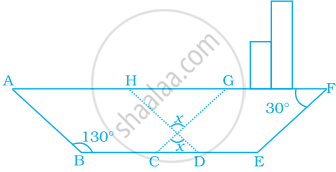
नीचे दिये गये एक जहाज कौँ आकृति में, ABDH और CEFG दो समांतर चतुर्भुज हैं। x का मान ज्ञात कीजिए।
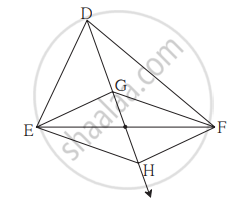
आकृति में, बिंदु G, ΔDEF की माध्यिकाओं का संगामी बिंदु है। किरण DG पर बिंदु H इस प्रकार लें कि D-G-H तथा DG = GH, हो तो सिद्ध कीजिए कि `square` GEHF समांतर चतुर्भुज है।
संलग्न आकृति में समांतर चतुर्भुज `square` ABCD की भुजाओं पर P, Q, R, S इस प्रकार है कि, AP = BQ = CR = DS तो सिद्ध कीजिए कि `square` PQRS समांतर चतुर्भुज है।

संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR