Advertisements
Advertisements
प्रश्न
P और Q क्रमश : एक समांतर चतुर्भुज ABCD की सम्मुख AD और BC भुजाओं पर स्थित बिंदु इस प्रकार हैं कि PQ विकण AC और BD के प्रतिच्छेद बिंदु O से होकर जाता है। सिद्ध कीजिए कि PQ बिंदु O पर समद्विभाजित हो जाता है।
उत्तर
दिया गया है - ABCD एक समांतर चतुर्भुज है जिसके विकर्ण परस्पर O पर समद्विभाजित करते हैं।
दर्शाना है - PQ, O पर समद्विभाजित है।
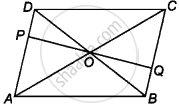
∆ODP और ΔOBQ में,
∠BOQ = ∠POD ...[चूंकि, शीर्षाभिमुख कोण]
∠OBQ = ∠ODP ...[वैकल्पिक आंतरिक कोण]
और OB = OD ...[दिया गया है।]
∴ ΔODP ≅ ΔOBQ ...[ASA सर्वांगसमता नियम द्वारा]
∴ OP = OQ ...[CPCT नियम द्वारा]
इसलिए, PQ, O पर समद्विभाजित है।
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
एक समांतर चतुर्भुज का एक विकर्ण उसके एक कोण को समद्विभाजित करता है। सिद्ध कीजिए कि यह समांतर चतुर्भुज एक समचतुर्भुज है।
P और Q क्रमश : एक समांतर चतुर्भुज ABCD की सम्मुख AB और CD भुजाओं के मध्य-बिंदु हैं। AQ, DP को S पर प्रतिच्छेद करता है तथा BQ, CP को R पर प्रतिच्छेद करता है। सिद्ध कीजिए कि PQRS एक समांतर चतुर्भुज है।
सिद्ध कीजिए कि किसी समलंब के विकर्णों के मध्य-बिंदुओं को मिलाने वाली रेखा उस समलंब की समांतर भुजाओं के समांतर होती है।
