Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि किसी समलंब के विकर्णों के मध्य-बिंदुओं को मिलाने वाली रेखा उस समलंब की समांतर भुजाओं के समांतर होती है।
उत्तर
दिया गया है - मान लीजिए ABCD एक समलंब है जिसमें AB || DC और मान लीजिए कि M और N क्रमश : विकर्ण AC और BD के मध्य-बिंदु हैं।
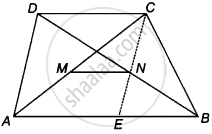
सिद्ध करना है - MN || AB || CD
रचना - CN को मिलाइए और इसे बढ़ाकर AB को E पर मिलाइए।
ΔCDN और ΔEBN में, हमारे पास है।
DN = BN ...[चूँकि N, BD का मध्य-बिंदु है।]
∠DCN = ∠BEN ...[वैकल्पिक आंतरिक कोण]
और ∠CDN = ∠EBN ...[वैकल्पिक आंतरिक कोण]
∴ ΔCDN ≅ ΔEBN ...[AAS सर्वांगसमता नियम द्वारा]
∴ DC = EB और CN = NE ...[CPCT नियम द्वारा]
इस प्रकार, ΔCAE में, बिंदु M और N क्रमश : AC और CE के मध्य-बिंदु हैं।
∴ MN || AE ...[मध्य-बिंदु प्रमेय द्वारा]
⇒ MN || AB || CD
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
एक समांतर चतुर्भुज का एक विकर्ण उसके एक कोण को समद्विभाजित करता है। सिद्ध कीजिए कि यह समांतर चतुर्भुज एक समचतुर्भुज है।
P और Q क्रमश : एक समांतर चतुर्भुज ABCD की सम्मुख AB और CD भुजाओं के मध्य-बिंदु हैं। AQ, DP को S पर प्रतिच्छेद करता है तथा BQ, CP को R पर प्रतिच्छेद करता है। सिद्ध कीजिए कि PQRS एक समांतर चतुर्भुज है।
P और Q क्रमश : एक समांतर चतुर्भुज ABCD की सम्मुख AD और BC भुजाओं पर स्थित बिंदु इस प्रकार हैं कि PQ विकण AC और BD के प्रतिच्छेद बिंदु O से होकर जाता है। सिद्ध कीजिए कि PQ बिंदु O पर समद्विभाजित हो जाता है।
