Advertisements
Advertisements
प्रश्न
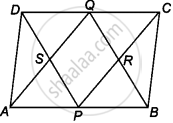
P और Q क्रमश : एक समांतर चतुर्भुज ABCD की सम्मुख AB और CD भुजाओं के मध्य-बिंदु हैं। AQ, DP को S पर प्रतिच्छेद करता है तथा BQ, CP को R पर प्रतिच्छेद करता है। सिद्ध कीजिए कि PQRS एक समांतर चतुर्भुज है।
उत्तर
दिया गया है - एक समांतर चतुर्भुज ABCD में, P और Q क्रमश : AS और CD के मध्य-बिंदु हैं।
दर्शाना है - PRQS एक समांतर चतुर्भुज है।
उपपत्ति - चूँकि, ABCD एक समांतर चतुर्भुज है।
AB || CD
⇒ AP || QC
साथ ही, AB = DC
`1/2`AB = `1/2`DC ...[दोनों पक्षों को 2 से विभाजित करने पर]
⇒ AP = QC ...[चूँकि, P और Q, AB और DC के मध्य-बिंदु हैं।]
अब, AP || QC और AP = QC
इस प्रकार, APCQ एक समांतर चतुर्भुज है।
∴ AQ || PC या SQ || PR ...(i)
दोबारा, AB || DC या BP || DQ
साथ ही, AB = DC
⇒ `1/2`AB = `1/2`DC ...[दोनों पक्षों को 2 से विभाजित करने पर]
⇒ BP = QD ...[चूँकि, P और Q, AB और DC के मध्य-बिंदु हैं।]
अब, BP || QD और BP = QD
इसलिए, BPDQ एक समांतर चतुर्भुज है।
∴ PD || BQ या PS || QR ...(ii)
समीकरण (i) और (ii) से,
SQ || RP और PS || QR
इसलिए, PRQS एक समांतर चतुर्भुज है।
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
एक समांतर चतुर्भुज का एक विकर्ण उसके एक कोण को समद्विभाजित करता है। सिद्ध कीजिए कि यह समांतर चतुर्भुज एक समचतुर्भुज है।
P और Q क्रमश : एक समांतर चतुर्भुज ABCD की सम्मुख AD और BC भुजाओं पर स्थित बिंदु इस प्रकार हैं कि PQ विकण AC और BD के प्रतिच्छेद बिंदु O से होकर जाता है। सिद्ध कीजिए कि PQ बिंदु O पर समद्विभाजित हो जाता है।
सिद्ध कीजिए कि किसी समलंब के विकर्णों के मध्य-बिंदुओं को मिलाने वाली रेखा उस समलंब की समांतर भुजाओं के समांतर होती है।
