Advertisements
Advertisements
प्रश्न
एक समांतर चतुर्भुज का एक विकर्ण उसके एक कोण को समद्विभाजित करता है। सिद्ध कीजिए कि यह समांतर चतुर्भुज एक समचतुर्भुज है।
उत्तर
दिया गया है - मान लीजिए ABCD एक समांतर चतुर्भुज है और विकर्ण AC कोण A को समद्विभाजित करता है।
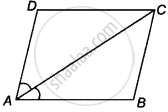
∴ ∠CAB = ∠CAD ...(i)
दर्शाना है - ABCD एक समचतुर्भुज है।
उपपत्ति - चूँकि, ABCD एक समांतर चतुर्भुज है, इसलिए AB || CD और AC एक तिर्यक रेखा है।
∴ ∠CAB = ∠ACD ...[वैकल्पिक आंतरिक कोण]
इसलिए, ∠ACD = ∠ACB [∵ ∠CAB = ∠CAD, दिया गया है।] ...(ii)
साथ ही, ∠A = ∠C ...[समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।]
⇒ `1/2`∠A = `1/2`∠C ...[दोनों पक्षों को 2 से विभाजित करने पर]
⇒ ∠DAC = ∠DCA ...[समीकरण (i) और (ii) से]
⇒ CD = AD ...[समान कोणों की सम्मुख भुजाएँ बराबर होती हैं।]
लेकिन AB = CD और AD = BC ...[समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।]
∴ AB = BC = CD = AD
इस प्रकार, सभी भुजाएँ समान हैं।
इसलिए, ABCD एक समचतुर्भुज है।
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
P और Q क्रमश : एक समांतर चतुर्भुज ABCD की सम्मुख AB और CD भुजाओं के मध्य-बिंदु हैं। AQ, DP को S पर प्रतिच्छेद करता है तथा BQ, CP को R पर प्रतिच्छेद करता है। सिद्ध कीजिए कि PQRS एक समांतर चतुर्भुज है।
P और Q क्रमश : एक समांतर चतुर्भुज ABCD की सम्मुख AD और BC भुजाओं पर स्थित बिंदु इस प्रकार हैं कि PQ विकण AC और BD के प्रतिच्छेद बिंदु O से होकर जाता है। सिद्ध कीजिए कि PQ बिंदु O पर समद्विभाजित हो जाता है।
सिद्ध कीजिए कि किसी समलंब के विकर्णों के मध्य-बिंदुओं को मिलाने वाली रेखा उस समलंब की समांतर भुजाओं के समांतर होती है।
