Advertisements
Advertisements
प्रश्न
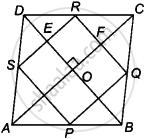
P, Q, R और S एक चतुर्भुज ABCD की क्रमश : AB, BC, CD और DA भुजाओं के मध्य-बिंदु हैं, जिसमें AC = BD और AC ⊥ BD है। सिद्ध कीजिए कि PQRS एक वर्ग है।
उत्तर
दिया गया है - चतुर्भुज ABCD में, P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं।
साथ ही, AC = BD और AC ⊥ BD।
सिद्ध करना है - PQRS एक वर्ग है।
उपपत्ति - अब, ΔADC में, S और R भुजाओं AD और DC के मध्य-बिंदु हैं, तो मध्य-बिंदु प्रमेय के अनुसार,
SR || AC और SR = `1/2` AC ...(i)
ΔABC में, P और Q, AB और BC के मध्य-बिंदु हैं, तो मध्य-बिंदु प्रमेय के अनुसार,
PQ || AC और PQ = `1/2` AC ...(ii)
समीकरण (i) और (ii) से,
PQ || SR और PQ = SR = `1/2` AC ...(iii)
इसी प्रकार, △ABD में, मध्य-बिंदु प्रमेय द्वारा,
SP || BD और SP = `1/2` BD = `1/2` AC [दिया गया है, AC = BD] ...(iv)
और ΔBCD, मध्य-बिंदु प्रमेय द्वारा,
RQ || BD और RQ = `1/2` BD = `1/2` AC [दिया गया है, BD = AC] ...(v)
समीकरण (iv) और (v) से,
SP = RQ = `1/2` AC ...(vi)
समीकरण (iii) और (vi) से,
PQ = SR = SP = RQ
इस प्रकार, चारों भुजाएँ बराबर हैं।
अब, चतुर्भुज OERF में,
OE || FR और OF || ER
∴ ∠EOF = ∠ERF = 90° ...[∵ AC ⊥ DB ⇒ ∠DOC = ∠EOF = 90° समांतर चतुर्भुज के सम्मुख कोणों के रूप में]
∴ ∠QRS = 90°
इसी प्रकार, ∠RQS = 90°
इसलिए, PQRS एक वर्ग है।
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
P, Q, R और S क्रमश : एक चतुर्भुज ABCD की AB, BC, CD और DA भुजाओं के मध्य-बिंदु हैं, जिसमें AC = BD है। सिद्ध कीजिए कि PQRS एक समचतुर्भज है।
P, Q, R और S क्रमश : एक चतुर्भुज ABCD की AB, BC, CD और DA भुजाओं के मध्य-बिंदु हैं, जिसमें AC ⊥ BD है। सिद्ध कीजिए कि PQRS एक आयत है।
ABCD एक चतुर्भुज है, जिसमें AB || DC और AD = BC है। सिद्ध कीजिए कि ∠A = ∠B और ∠C = ∠D है।
निम्नलिखित आकृति में, AB || DE, AB = DE, AC || DF तथा AC = DF है। सिद्ध कीजिए कि BC || EF और BC = EF है।
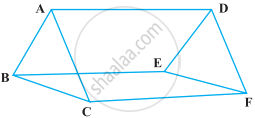
E और F क्रमश : एक समलंब ABCD की असमांतर AD और BC भुजाओं के मध्य-बिंदु हैं। सिद्ध कीजिए कि EF || AB और EF = `1/2` (AB + CD) है।
[संकेत : BE को मिलाइए तथा इसे बढ़ाई गई CD से G पर मिलने के लिए बढ़ाइए।]
D, E और F क्रमश : एक त्रिभुज ABC की AB, BC और CA भुजाओं के मध्य-बिंदु हैं। सिद्ध कीजिए D, E और F बिंदुओं को मिलाने से त्रिभुज ABC चार सर्वांगसम त्रिभुजों में बँट जाता है।
