Advertisements
Advertisements
प्रश्न
एक चतुर्भुज की कच्ची आकृति खीचिए जो समांतर चतुर्भुज न हो परंतु जिसके दो सम्मुख कोणों के माप बराबर हों।
उत्तर
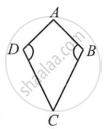
हम एक पतंग का चित्र बना सकते हैं जिसमें ठीक दो सम्मुख कोण बराबर हों। अतः ∠D = ∠B.
APPEARS IN
संबंधित प्रश्न
निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:

किसी समांतर चतुर्भुज के दो आसन्न कोनो के माप बराबर हैं। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
बताइए कैसे एक वर्ग एक समांतर चतुर्भुज है।
एक समांतर चतुर्भुज के विकर्ण परस्पर लंब होते हैं। क्या यह कथन सत्य है? अपने उत्तर के लिए कारण दीजिए।
E एक समलंब ABCD की भुजा AD का मध्य-बिंदु है, जिसमें AB || DC है। E से होकर AB के समांतर खींची गई रेखा BC को F पर प्रतिच्छेद करती है। दर्शाइए कि F भुजा BC का मध्य-बिंदु है। [संकेत : AC को मिलाइए]
यदि किसी समांतर चतुर्भुज के दो आसन्न कोण (5x − 5)∘ और (10x + 35)∘ हैं, तो इन कोणों का अनुपात होगा –
यदि एक चतुर्भुज के सम्मुख कोण बराबर हों, तो वह अवश्य ही समांतर चतुर्भुज होगा।
किसी चतुर्भुज के विकर्णों का प्रतिच्छेद बिंदु इनमें से एक को 1: 2 के अनुपात में विभाजित करता है। क्या यह एक समांतर चतुर्भुज होगा? क्यों और क्यों नहीं?
नीचे दिये समांतर चतुर्भुज PQRS में, O विकर्ण SQ का मध्य बिंदु है। ∠S, ∠R, PQ, QR और विकर्ण PR ज्ञात कीजिए।
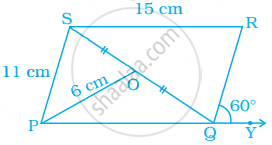
निम्न समांतर चतुर्भुज में, x और y के मान ज्ञात कीजिए –
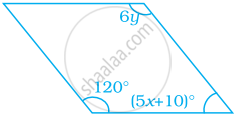
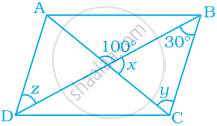
ABCD एक समांतर चतुर्भुज है। x, y और z के मान ज्ञात कीजिए।
किसी समांतर चतुर्भुज का एक विकर्ण उसके एक कोण को समद्विभाजित करता है। क्या वह दूसरे कोण को भी समद्विभाजित करेगा? कारण दीजिए।
ABCD एक समांतर चतुर्भुज है। भुजा AB और AD पर क्रमशः बिंदु P और Q इस प्रकार लिये गये हैं कि एक समांतर चतुर्भुज PRQA बनता है। यदि ∠C = 45∘ है, तो ∠R ज्ञात कीजिए।
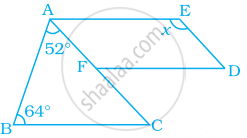
निम्न आकृति में, FD || BC || AE है और AC || ED है। x का मान ज्ञात कीजिए –
एक समांतर चतुर्भुज HOME की रचना कीजिए, जिसमें HO = 6 cm, HE = 4 cm और OE = 3 cm है।
किसी समांतर चतुर्भुज के दो संलग्न कोणों के मापों का अनुपात 1 : 2 हो तो उस समांतर चतुर्भुज के सभी कोणों के माप ज्ञात कीजिए।
समांतर चतुर्भुज की दो संलग्न भुजाओं का अनुपात 3 : 4 है। उसकी परिमिति 112 सेमी हो तो उसकी प्रत्येक भुजा की लंबाई ज्ञात कीजिए।
संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR