Advertisements
Advertisements
प्रश्न
एक समांतर चतुर्भुज HOME की रचना कीजिए, जिसमें HO = 6 cm, HE = 4 cm और OE = 3 cm है।
उत्तर
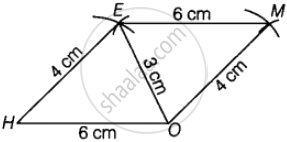
रचना के चरण -
चरण I - HO = 6 सेमी खींचिए।
चरण II - H को केंद्र मानकर और HE = 4 सेमी त्रिज्या लेकर एक चाप लगाइए।
चरण III - O को केंद्र मानकर और OE = 3 सेमी त्रिज्या लेकर, चरण II में खींचे गए चाप को E पर प्रतिच्छेद करते हुए एक चाप लगाएं।
चरण IV - E को केंद्र मानकर और EM = 6 सेमी त्रिज्या लेकर, भुजा HE के विपरीत एक चाप खींचें।
चरण V - O को केंद्र मानकर और त्रिज्या OM = 4 सेमी, चरण IV में खींचे गए चाप को M पर प्रतिच्छेद करते हुए एक चाप बनाएं।
चरण VI - HE, OE, EM और OM को मिलाइए।
अतः, HOME अभीष्ट समांतर चतुर्भुज है।
APPEARS IN
संबंधित प्रश्न
यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि:
- ABCD एक वर्ग है।
- विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
ABCD एक समांतर चतुर्भुज है। प्रत्येक कथन को परिभाषा या प्रयोग किए गए गुण द्वारा पूरा कीजिए :

- AD = ______
- ∠DCB = ______
- OC = ______
- m∠DAB + m∠CDA = ______
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि AB = DC = 8 cm, AD = 4 cm और BC = 4.4 cm?
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠A = 70° और ∠C = 65°?
एक चतुर्भुज की कच्ची आकृति खीचिए जो समांतर चतुर्भुज न हो परंतु जिसके दो सम्मुख कोणों के माप बराबर हों।
निम्नलिखित के लिए कारण दीजिए:
वर्ग, आयत, समांतर चतुर्भुज और समचतुर्भुज में से प्रत्येक एक चतुर्भुज भी है।
E एक समलंब ABCD की भुजा AD का मध्य-बिंदु है, जिसमें AB || DC है। E से होकर AB के समांतर खींची गई रेखा BC को F पर प्रतिच्छेद करती है। दर्शाइए कि F भुजा BC का मध्य-बिंदु है। [संकेत : AC को मिलाइए]
एक समांतर चतुर्भुज ABCD में, AB = 10 cm और AD = 6 cm है। ∠A का समद्विभाजक DC से E पर मिलता है तथा AE और BC बढ़ाने पर F पर मिलते हैं। CF की लंबाई ज्ञात कीजिए।
निम्न में से कौन एक समांतर चतुर्भुज का गुण है?
यदि किसी समांतर चतुर्भुज के दो आसन्न कोण (5x − 5)∘ और (10x + 35)∘ हैं, तो इन कोणों का अनुपात होगा –
नीचे दी गयी आकृति में, ABCD और BDCE एक ही आधार DC पर दो समांतर चतुर्भुज हैं। यदि BC ⊥ BD है, तो ∠BEC बराबर है –
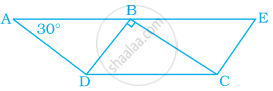
सभी आयत समांतर चतुर्भुज होते हैं।
किसी चतुर्भुज के विकर्णों का प्रतिच्छेद बिंदु इनमें से एक को 1: 2 के अनुपात में विभाजित करता है। क्या यह एक समांतर चतुर्भुज होगा? क्यों और क्यों नहीं?
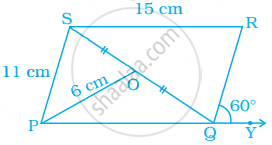
नीचे दिये समांतर चतुर्भुज PQRS में, O विकर्ण SQ का मध्य बिंदु है। ∠S, ∠R, PQ, QR और विकर्ण PR ज्ञात कीजिए।
एक समांतर चतुर्भुज MODE में, ∠M कोण ∠O के समद्विभाजक Q पर मिलते हैं। ∠MQO की माप ज्ञात कीजिए।
एक समांतर चतुर्भुज के अधिक कोण वाले शीर्ष से खींचे गये दो शीर्षलंबों के बीच का कोण 45∘ है। इस समांतर चतुर्भुज के कोण ज्ञात कीजिए।
ABCD एक समांतर चतुर्भुज है। भुजा AB और AD पर क्रमशः बिंदु P और Q इस प्रकार लिये गये हैं कि एक समांतर चतुर्भुज PRQA बनता है। यदि ∠C = 45∘ है, तो ∠R ज्ञात कीजिए।
एक समांतर चतुर्भुज की रचना कीजिए जिसकी एक भुजा 4 cm और दोनों विकर्ण 5.6 cm और 7 cm हों। दूसरी भुजा को मापिए।
