Advertisements
Advertisements
प्रश्न
आकृति में `square` PQRS तथा `square` ABCR दो समांतर चतुर्भुज है। ∠P = 110° तो `square `ABCR के सभी कोणों के माप ज्ञात कीजिए।

उत्तर
`square` PQRS समांतर चतुर्भुज है। ....( दिया है।)
∴ ∠R = ∠P ....( समांतर चतुर्भुज के सम्मुख कोण)
∴ ∠P = 110° ...( दिया है।)
∴ ∠R = 110° ....(S-A-R, R-C-Q)
`square` ABCR समांतर चतुर्भुज है। ....( दिया है।)
∴ ∠R = ∠B ....( समांतर चतुर्भुज के सम्मुख कोण)
∴ ∠B = 110° ...( दिया है।)
∴ ∠A + ∠R = 180° ....(समांतर चतुर्भुज के क्रमिक कोण संपूरक होते हैं।)
∴ ∠A + 110° = 180°
∴ ∠A= 180°- 110°
∴ ∠A = 70°
∴ ∠C = ∠A ....( समांतर चतुर्भुज के सम्मुख कोण)
∴ ∠C = 70°
APPEARS IN
संबंधित प्रश्न
यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:

क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠A = 70° और ∠C = 65°?
∆ABC में, AB = 5 cm, BC = 8 cm और CA = 7 cm हैं। यदि D और E क्रमश : AB और BC के मध्य-बिंदु हैं, तो DE की लंबाई निर्धारित कीजिए।
E एक समलंब ABCD की भुजा AD का मध्य-बिंदु है, जिसमें AB || DC है। E से होकर AB के समांतर खींची गई रेखा BC को F पर प्रतिच्छेद करती है। दर्शाइए कि F भुजा BC का मध्य-बिंदु है। [संकेत : AC को मिलाइए]
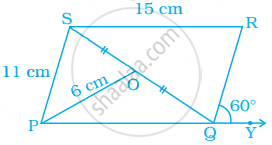
नीचे दिये समांतर चतुर्भुज PQRS में, O विकर्ण SQ का मध्य बिंदु है। ∠S, ∠R, PQ, QR और विकर्ण PR ज्ञात कीजिए।
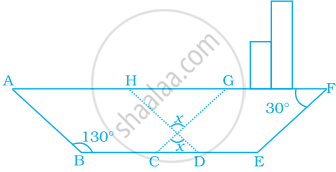
नीचे दिये गये एक जहाज कौँ आकृति में, ABDH और CEFG दो समांतर चतुर्भुज हैं। x का मान ज्ञात कीजिए।
एक समांतर चतुर्भुज ABCD की रचना कीजिए, जिसमें AB = 4cm, BC = 5 cm और ∠B = 60∘ है।
एक समांतर चतुर्भुज HOME की रचना कीजिए, जिसमें HO = 6 cm, HE = 4 cm और OE = 3 cm है।
सिद्ध कीजिए कि एक समांतर चतुर्भुज के कोणों के समद्विभाजकों द्वारा बना चतुर्भुज एक आयत होता है।
