Advertisements
Advertisements
प्रश्न
ABCD एक समचतुर्भुज है, जिसमें D से AB पर शीर्षलंब AB को समद्विभाजित करता है। समचतुर्भुज के कोण ज्ञात कीजिए।
उत्तर
माना समचतुर्भुज की भुजाएँ AB = BC = CD = DA = x हैं।
अब, DB से जुड़ें।
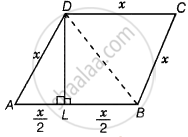
ΔALD और ΔBLD में,
∠DLA = ∠DLB = 90°
AL = BL = `x/2` ...[चूंकि, DL, AB का लंब समद्विभाजक है।]
और DL = DL ...[सामान्य पक्ष]
∴ ΔALD ≅ ΔBLD ...[SAS सर्वांगसमता नियम द्वारा]
AD = BD ...[CPCT द्वारा]
अब, △ADB में,
तो, ΔADB एक समबाहु त्रिभुज है।
∴ ∠A = ∠ADB = ∠ABD = 60°
इसी प्रकार, ∆DBC एक समबाहु त्रिभुज है।
∴ ∠C = ∠BDC = ∠BC = 60°
साथ ही, ∠A = ∠C
∴ ∠D = ∠B = 180° – 60° = 120° ...[चूंकि आंतरिक कोणों का योग 180° है।]
APPEARS IN
संबंधित प्रश्न
समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति में)। दर्शाइए कि
- यह ∠C को भी समद्विभाजित करता है।
- ABCD एक समचतुर्भुज है

निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:

क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠D +∠B = 180°?
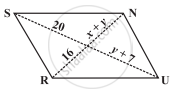
निम्न आकृति RUNS समांतर चतुर्भुज हैं। x तथा y ज्ञात कीजिए (लंबाई cm में है) :
निम्नलिखित आकृति में, यह दिया है कि BDEF और FDCE समांतर चतुर्भुज हैं। क्या आप कह सकते हैं कि BD = CD है? क्यों और क्यों नहीं?

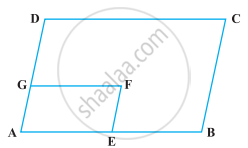
निम्नलिखित आकृति में, ABCD और AEFG दो समांतर चतुर्भुज हैं यदि ∠C = 55° है, तो ∠F निर्धारित कीजिए।
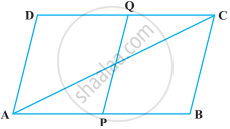
एक समांतर चतुर्भुज ABCD की सम्मुख भुजाओं AB और CD पर क्रमश : बिंदु P और Q इस प्रकार लिए गए हैं कि AP = CQ है। (आकृति)। दर्शाइए कि AC और PQ परस्पर समद्विभाजित करते हैं।
एक समांतर चतुर्भुज की आसन्न भुजाएँ 5 cm और 9 cm है। उसका परिमाप ______ है।
एक समांतर चतुर्भुज ABCD की रचना कीजिए, जिसमें AB = 4cm, BC = 5 cm और ∠B = 60∘ है।
किसी समांतर चतुर्भुज के दो संलग्न कोणों के मापों का अनुपात 1 : 2 हो तो उस समांतर चतुर्भुज के सभी कोणों के माप ज्ञात कीजिए।
