Advertisements
Advertisements
प्रश्न
समांतर चतुर्भुज ABCD के विकर्ण, AC पर बिंदु E और F इस प्रकार स्थित हैं कि AE = CF है। दर्शाइए कि BFDE एक समांतर चतुर्भुज है।
उत्तर
दिया गया है - ABCD एक समांतर चतुर्भुज है और AE = CF है।
दिखाने के लिए - OE = OF
रचना - BD को मिलाइए, AC को बिंदु O पर मिलिए।
उपपत्ति - चूँकि, समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।
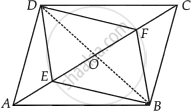
∴ OA = OC
और OD = OB
अब, OA = OC
और AE = CF ...[दिया गया है।]
⇒ OA – AE = OC – CF
⇒ OE = OF
इस प्रकार, BFDE एक चतुर्भुज है जिसके विकर्ण एक दूसरे को समद्विभाजित करते हैं।
अतः, BFDE एक समांतर चतुर्भुज है।
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠D +∠B = 180°?
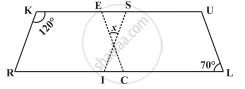
दी गई आकृति में RISK तथा CLUE दोनों समांतर चतुर्भुज हैं, x का मान ज्ञात कीजिए।
बताइए कैसे एक वर्ग एक समांतर चतुर्भुज है।
एक समांतर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर प्रतिच्छेद करते हैं। यदि OA = 3 cm और OD = 2 cm है, तो AC और BD की लंबाई ज्ञात कीजिए।
निम्न में से कौन एक समांतर चतुर्भुज का गुण है?
यदि किसी समांतर चतुर्भुज के दो आसन्न कोण (5x − 5)∘ और (10x + 35)∘ हैं, तो इन कोणों का अनुपात होगा –
किसी समांतर चतुर्भुज के एक अधिक कोण वाले शीर्ष से खींचे गये दो शीर्षलंबों के बीच का कोण 30∘ है। उस अधिक कोण की माप है –
एक समांतर चतुर्भुज ABCD की रचना कीजिए, जिसमें AB = 4cm, BC = 5 cm और ∠B = 60∘ है।
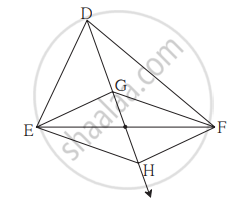
आकृति में, बिंदु G, ΔDEF की माध्यिकाओं का संगामी बिंदु है। किरण DG पर बिंदु H इस प्रकार लें कि D-G-H तथा DG = GH, हो तो सिद्ध कीजिए कि `square` GEHF समांतर चतुर्भुज है।
संलग्न आकृति में समांतर चतुर्भुज `square` ABCD की भुजाओं पर P, Q, R, S इस प्रकार है कि, AP = BQ = CR = DS तो सिद्ध कीजिए कि `square` PQRS समांतर चतुर्भुज है।

