Advertisements
Advertisements
प्रश्न
समांतर चतुर्भुज ABCD के विकर्ण, AC पर बिंदु E और F इस प्रकार स्थित हैं कि AE = CF है। दर्शाइए कि BFDE एक समांतर चतुर्भुज है।
उत्तर
दिया गया है - ABCD एक समांतर चतुर्भुज है और AE = CF है।
दिखाने के लिए - OE = OF
रचना - BD को मिलाइए, AC को बिंदु O पर मिलिए।
उपपत्ति - चूँकि, समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।
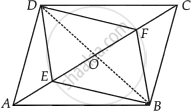
∴ OA = OC
और OD = OB
अब, OA = OC
और AE = CF ...[दिया गया है।]
⇒ OA – AE = OC – CF
⇒ OE = OF
इस प्रकार, BFDE एक चतुर्भुज है जिसके विकर्ण एक दूसरे को समद्विभाजित करते हैं।
अतः, BFDE एक समांतर चतुर्भुज है।
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति में)। दर्शाइए कि
- यह ∠C को भी समद्विभाजित करता है।
- ABCD एक समचतुर्भुज है

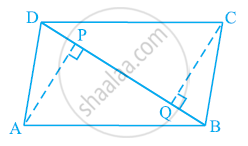
ABCD एक समांतर चतुर्भज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं (देखिए आकृति में)। दर्शाइए कि
- ΔAPB ≅ ΔCQD
- AP = CQ
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠D +∠B = 180°?
किसी समांतर चतुर्भुज के दो आसन्न कोनो के माप बराबर हैं। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
एक चतुर्भुज का नाम बताइए जिसके विकर्ण एक दूसरे को समद्विभाजित करते है।
निम्नलिखित के लिए कारण दीजिए:
वर्ग एक समांतर चतुर्भुज भी है।
एक समांतर चतुर्भुज के विकर्ण परस्पर लंब होते हैं। क्या यह कथन सत्य है? अपने उत्तर के लिए कारण दीजिए।
एक समांतर चतुर्भुज MODE में, ∠M कोण ∠O के समद्विभाजक Q पर मिलते हैं। ∠MQO की माप ज्ञात कीजिए।
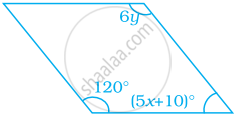
निम्न समांतर चतुर्भुज में, x और y के मान ज्ञात कीजिए –
आकृति में `square` PQRS तथा `square` ABCR दो समांतर चतुर्भुज है। ∠P = 110° तो `square `ABCR के सभी कोणों के माप ज्ञात कीजिए।

