Advertisements
Advertisements
प्रश्न
किसी समांतर चतुर्भुज के एक अधिक कोण वाले शीर्ष से खींचे गये दो शीर्षलंबों के बीच का कोण 30∘ है। उस अधिक कोण की माप है –
विकल्प
100∘
150∘
105°
120°
उत्तर
150∘
स्पष्टीकरण -
माना EC और FC शीर्षलंब हैं और ∠ECF = 30° है।
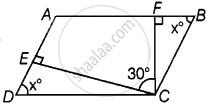
माना ∠EDC = x = ∠FBC
तो, ∠ECD = 90° – x और ∠BCF = 90° – x
तो, समांतर चतुर्भुज के गुण द्वारा,
∠ADC + ∠DCB = 180°
∠ADC + (∠ECD + ∠ECF + ∠BCF) = 180°
⇒ x + 90° – x + 30° + 90° – x = 180°
⇒ – x = 180° – 210° = – 30°
⇒ x = 30°
अतः, ∠DCB = 30° + 60° + 60° = 150°
APPEARS IN
संबंधित प्रश्न
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि:
- ABCD एक वर्ग है।
- विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
ABCD एक समांतर चतुर्भुज है। प्रत्येक कथन को परिभाषा या प्रयोग किए गए गुण द्वारा पूरा कीजिए :

- AD = ______
- ∠DCB = ______
- OC = ______
- m∠DAB + m∠CDA = ______
निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:
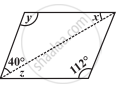
किसी समांतर चतुर्भुज के दो आसन्न कोणों का अनुपात 3 : 2 है। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
एक चतुर्भुज का नाम बताइए जिसके विकर्ण एक दूसरे को समद्विभाजित करते है।
निम्नलिखित के लिए कारण दीजिए:
वर्ग, आयत, समांतर चतुर्भुज और समचतुर्भुज में से प्रत्येक एक चतुर्भुज भी है।
निम्नलिखित के लिए कारण दीजिए:
वर्ग एक समांतर चतुर्भुज भी है।
एक समांतर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर प्रतिच्छेद करते हैं। यदि OA = 3 cm और OD = 2 cm है, तो AC और BD की लंबाई ज्ञात कीजिए।
एक चतुर्भुज ABCD के विकर्ण परस्पर समद्विभाजित करते हैं। यदि ∠A = 35° है, तो ∠B निर्धारित कीजिए।
एक चतुर्भुज ABCD के सम्मुख कोण बराबर हैं। यदि AB = 4 cm है, तो CD निर्धारित कीजिए।
ABCD एक समलंब है जिसमें AB || DC और ∠A = ∠B = 45° है। इस समलंब के कोण C और D ज्ञात कीजिए।
E एक समलंब ABCD की भुजा AD का मध्य-बिंदु है, जिसमें AB || DC है। E से होकर AB के समांतर खींची गई रेखा BC को F पर प्रतिच्छेद करती है। दर्शाइए कि F भुजा BC का मध्य-बिंदु है। [संकेत : AC को मिलाइए]
नीचे दी गयी आकृति में, ABCD और BDCE एक ही आधार DC पर दो समांतर चतुर्भुज हैं। यदि BC ⊥ BD है, तो ∠BEC बराबर है –
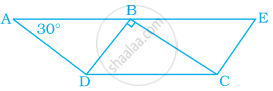
एक समांतर चतुर्भुज की आसन्न भुजाएँ 5 cm और 9 cm है। उसका परिमाप ______ है।
सभी आयत समांतर चतुर्भुज होते हैं।
एक समांतर चतुर्भुज HOME की रचना कीजिए, जिसमें HO = 6 cm, HE = 4 cm और OE = 3 cm है।
किसी समांतर चतुर्भुज के दो संलग्न कोणों के मापों का अनुपात 1 : 2 हो तो उस समांतर चतुर्भुज के सभी कोणों के माप ज्ञात कीजिए।
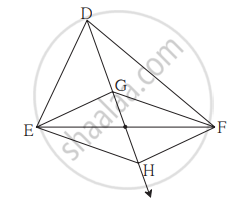
आकृति में, बिंदु G, ΔDEF की माध्यिकाओं का संगामी बिंदु है। किरण DG पर बिंदु H इस प्रकार लें कि D-G-H तथा DG = GH, हो तो सिद्ध कीजिए कि `square` GEHF समांतर चतुर्भुज है।