Advertisements
Advertisements
प्रश्न
समांतर ABCD में, ∠A का समद्विभाजक BC को समद्विभाजित करता है। क्या कोण B का समद्विभाजक AD को भी समद्विभाजित करता है? कारण दीजिए।
उत्तर
दिया गया है, ABCD एक समांतर चतुर्भुज है, जो ∠A का समद्विभाजक है, BC को F पर समद्विभाजित करता है, अर्थात ∠1 = ∠2, CF = FB।
खींचना FE || BA
रचना द्वारा ABFE एक समांतर चतुर्भुज है। ...[∵ FE || BA]
⇒ ∠1 = ∠6 ...[वैकल्पिक कोण]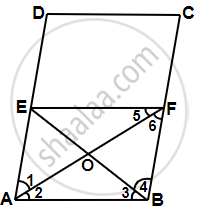
लेकिन ∠1 = ∠2 ...[दिया गया है।]
∴ ∠2 = ∠6
AB = FB [समान कोणों की सम्मुख भुजाएँ बराबर होती हैं।] ...(i)
∴ ABFE एक समचतुर्भुज है।
अब, ΔABO और ΔBOF में,
AB = BF ...[समीकरण (i) से]
BO = BO ...[सामान्य]
AO = FO ...[समचतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।]
∴ ΔABO ≅ ΔBOF ...[SSS द्वारा]
∠3 = ∠4 ...[CPCT द्वारा]
अब, BF = `1/2` BC ...[दिया गया है।]
⇒ BF = `1/2` AD ...[BC = AD]
⇒ AE = `1/2` AD ...[BF = AE]
∴ E, AD का मध्यबिंदु है।
APPEARS IN
संबंधित प्रश्न
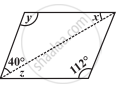
निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:

निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि AB = DC = 8 cm, AD = 4 cm और BC = 4.4 cm?
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠A = 70° और ∠C = 65°?
एक चतुर्भुज की कच्ची आकृति खीचिए जो समांतर चतुर्भुज न हो परंतु जिसके दो सम्मुख कोणों के माप बराबर हों।
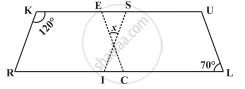
दी गई आकृति में RISK तथा CLUE दोनों समांतर चतुर्भुज हैं, x का मान ज्ञात कीजिए।
निम्नलिखित के लिए कारण दीजिए:
वर्ग एक समांतर चतुर्भुज भी है।
एक चतुर्भुज ABCD के सम्मुख कोण बराबर हैं। यदि AB = 4 cm है, तो CD निर्धारित कीजिए।
किसी समांतर चतुर्भुज के एक अधिक कोण वाले शीर्ष से खींचे गये दो शीर्षलंबों के बीच का कोण 30∘ है। उस अधिक कोण की माप है –
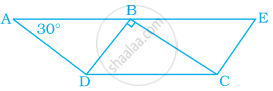
नीचे दी गयी आकृति में, ABCD और BDCE एक ही आधार DC पर दो समांतर चतुर्भुज हैं। यदि BC ⊥ BD है, तो ∠BEC बराबर है –
एक समांतर चतुर्भुज की आसन्न भुजाएँ 5 cm और 9 cm है। उसका परिमाप ______ है।
सभी आयत समांतर चतुर्भुज होते हैं।
यदि एक चतुर्भुज के सम्मुख कोण बराबर हों, तो वह अवश्य ही समांतर चतुर्भुज होगा।
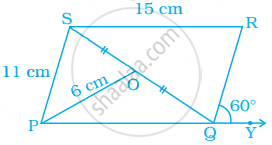
नीचे दिये समांतर चतुर्भुज PQRS में, O विकर्ण SQ का मध्य बिंदु है। ∠S, ∠R, PQ, QR और विकर्ण PR ज्ञात कीजिए।
एक समांतर चतुर्भुज MODE में, ∠M कोण ∠O के समद्विभाजक Q पर मिलते हैं। ∠MQO की माप ज्ञात कीजिए।
एक समांतर चतुर्भुज ABCD की रचना कीजिए, जिसमें AB = 4cm, BC = 5 cm और ∠B = 60∘ है।
सिद्ध कीजिए कि एक समांतर चतुर्भुज के कोणों के समद्विभाजकों द्वारा बना चतुर्भुज एक आयत होता है।
आकृति में `square` ABCD समांतर चतुर्भुज है। किरण AB पर बिंदु E इस प्रकार है कि BE = AB तो सिद्ध कीजिए कि रेखा ED यह रेख BC को बिंदु F पर समद्विभाजित करती है।

