Advertisements
Advertisements
प्रश्न
कोई वर्ग एक समद्विबाहु समकोण त्रिभुज के अंतर्गत इस प्रकार है कि वर्ग और त्रिभुज में एक कोण उभयनिष्ठ है। दर्शाइए कि वर्ग का शीर्ष जो उभयनिष्ठ कोण के शीर्ष के सम्मुख है कर्ण को समद्विभाजित करता है।
उत्तर
दिया है - एक समद्विबाहु त्रिभुज ABC में एक वर्ग ΔDEF बना हुआ है।
सिद्ध करना है - CE = BE
प्रमाण - एक समद्विबाहु ΔABC में,
∠A = 90°
और AB = AC ...(i)
चूँकि, ΔDEF एक वर्ग है।
AD = AF [वर्ग की सभी भुजाएँ बराबर होती हैं।] ...(ii)
समीकरण (ii) को समीकरण (i) से घटाने पर, हम पाते हैं।
AB – AD = AC – AF
BD = CF ...(iii)
अब, ΔCFE और ΔBDE में,
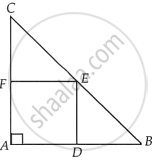
BD = CF ...[समीकरण (iii) से]
DE = EF ...[वर्ग की भुजाएँ]
और ∠CFE = ∠EDB ...[प्रत्येक 90°]
ΔCFE ≅ ΔBDE ...[SAS सर्वांगसमता नियम]
∴ CE = BE ...[CPCT द्वारा]
अतः, वर्ग का शीर्ष E कर्ण BC को समद्विभाजित करता है।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित आकृति में x (कोण की माप) ज्ञात कीजिए :
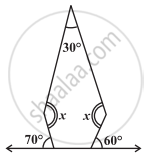
x + y + z + w ज्ञात कीजिए।
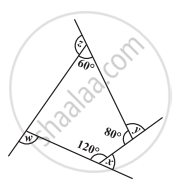
क्या किसी चतुर्भुज के सभी कोण अधिककोण हो सकते हैं? अपने उत्तर के लिए कारण दीजिए।
निम्नलिखित आकृति में, समांतर चतुर्भुज ABCD की भुजा BC पर एक बिंदु P इस प्रकार स्थित है। कि ∠BAP = ∠DAP है। सिद्ध कीजिए कि AD = 2CD है।
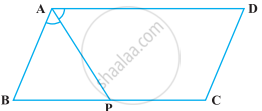
यदि किसी चतुर्भुज के तीन कोणों में से प्रत्येक कोण 75∘ के बराबर है, तो चौथा कोण है –
यदि एक चतुर्भुज के तीन कोणों में से प्रत्येक की माप 80∘ है, तब चौथे कोण की माप होगी –
चतुर्भुज के सभी ______ का योग 360∘ है।
चतुर्भुज के सभी कोणों का योग 180∘ होता है।
चतुर्भुज PQRS में, ∠P = 50∘, ∠Q = 50∘ और ∠R = 60∘ है। ∠S ज्ञात कीजिए। क्या यह चतुर्भुज उत्तल है या अवतल?
एक चतुर्भुज के तीन कोण बराबर हैं। चौथे कोण की माप 120∘ है। बराबर कोणों में से प्रत्येक की माप ज्ञात कीजिए।
