Advertisements
Advertisements
प्रश्न
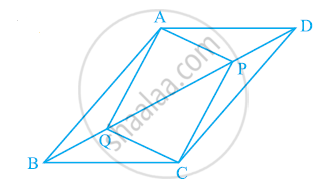
समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP = BQ है (देखिए आकृति में)। दर्शाइए कि
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ एक समांतर चतुर्भुज है।
उत्तर
(i) ΔAPD और ΔCQB में,
∠ADP = ∠CBQ ...(BC || AD के लिए एकांतर अंत: कोण)
AD = CB ...(समांतर चतुर्भुज ABCD की सम्मुख भुजाएँ)
DP = BQ ...(दिया गया है)
∴ ΔAPD ≅ ΔCQB ...(SAS सर्वांगसमता नियम का उपयोग करके)
(ii) जैसा कि हमने देखा था कि ΔAPD ≅ ΔCQB,
∴ AP = CQ ...(CPCT)
(iii) ΔAQB और ΔCPD में,
∠ABQ = ∠CDP ...(AB || CD के लिए एकांतर अंत: कोण)
AB = CD ...(समांतर चतुर्भुज ABCD की सम्मुख भुजाएँ)
BQ = DP ...(दिया गया है)
∴ ΔAQB ≅ ΔCPD ...(SAS सर्वांगसमता नियम का उपयोग करके)
(iv) जैसा कि हमने देखा था कि ΔAQB ≅ ΔCPD,
∴ AQ = CP ...(CPCT)
(v) (ii) और (iv) में प्राप्त परिणामों से,
AQ = CP और
AP = CQ
क्योंकि चतुर्भुज APCQ में सम्मुख भुजाएँ एक दूसरे के बराबर होती हैं, इसलिए APCQ एक समांतर चतुर्भुज है।
APPEARS IN
संबंधित प्रश्न
यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
ABCD एक समांतर चतुर्भुज है। प्रत्येक कथन को परिभाषा या प्रयोग किए गए गुण द्वारा पूरा कीजिए :

- AD = ______
- ∠DCB = ______
- OC = ______
- m∠DAB + m∠CDA = ______
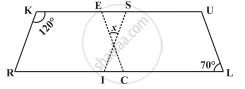
दी गई आकृति में RISK तथा CLUE दोनों समांतर चतुर्भुज हैं, x का मान ज्ञात कीजिए।
बताइए कैसे एक वर्ग एक समांतर चतुर्भुज है।
एक चतुर्भुज ABCD के सम्मुख कोण बराबर हैं। यदि AB = 4 cm है, तो CD निर्धारित कीजिए।
E एक समलंब ABCD की भुजा AD का मध्य-बिंदु है, जिसमें AB || DC है। E से होकर AB के समांतर खींची गई रेखा BC को F पर प्रतिच्छेद करती है। दर्शाइए कि F भुजा BC का मध्य-बिंदु है। [संकेत : AC को मिलाइए]
नीचे दी गयी आकृतियों में से कौन-सी आकृति निम्नलिखित गुणों को संतुष्ट करती है?
- सभी भुजाएँ बराबर हैं।
- सभी कोण समकोण हैं।
- सम्मुख भुजाएँ समांतर हैं।
यदि एक चतुर्भुज के सम्मुख कोण बराबर हों, तो वह अवश्य ही समांतर चतुर्भुज होगा।
समांतर ABCD में, ∠A का समद्विभाजक BC को समद्विभाजित करता है। क्या कोण B का समद्विभाजक AD को भी समद्विभाजित करता है? कारण दीजिए।
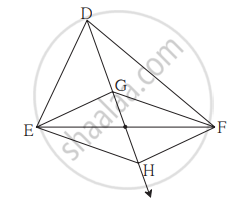
आकृति में, बिंदु G, ΔDEF की माध्यिकाओं का संगामी बिंदु है। किरण DG पर बिंदु H इस प्रकार लें कि D-G-H तथा DG = GH, हो तो सिद्ध कीजिए कि `square` GEHF समांतर चतुर्भुज है।