Advertisements
Advertisements
Question
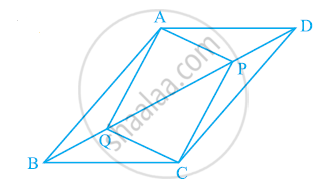
समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP = BQ है (देखिए आकृति में)। दर्शाइए कि
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ एक समांतर चतुर्भुज है।
Solution
(i) ΔAPD और ΔCQB में,
∠ADP = ∠CBQ ...(BC || AD के लिए एकांतर अंत: कोण)
AD = CB ...(समांतर चतुर्भुज ABCD की सम्मुख भुजाएँ)
DP = BQ ...(दिया गया है)
∴ ΔAPD ≅ ΔCQB ...(SAS सर्वांगसमता नियम का उपयोग करके)
(ii) जैसा कि हमने देखा था कि ΔAPD ≅ ΔCQB,
∴ AP = CQ ...(CPCT)
(iii) ΔAQB और ΔCPD में,
∠ABQ = ∠CDP ...(AB || CD के लिए एकांतर अंत: कोण)
AB = CD ...(समांतर चतुर्भुज ABCD की सम्मुख भुजाएँ)
BQ = DP ...(दिया गया है)
∴ ΔAQB ≅ ΔCPD ...(SAS सर्वांगसमता नियम का उपयोग करके)
(iv) जैसा कि हमने देखा था कि ΔAQB ≅ ΔCPD,
∴ AQ = CP ...(CPCT)
(v) (ii) और (iv) में प्राप्त परिणामों से,
AQ = CP और
AP = CQ
क्योंकि चतुर्भुज APCQ में सम्मुख भुजाएँ एक दूसरे के बराबर होती हैं, इसलिए APCQ एक समांतर चतुर्भुज है।
APPEARS IN
RELATED QUESTIONS
समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति में)। दर्शाइए कि
- यह ∠C को भी समद्विभाजित करता है।
- ABCD एक समचतुर्भुज है

निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:

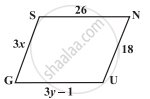
निम्न आकृति GUNS समांतर चतुर्भुज हैं। x तथा y ज्ञात कीजिए (लंबाई cm में है) :
एक समांतर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर प्रतिच्छेद करते हैं। यदि OA = 3 cm और OD = 2 cm है, तो AC और BD की लंबाई ज्ञात कीजिए।
चतुर्भुज ABCD में, ∠A + ∠D = 180° है। इस चतुर्भुज को कौन-सा विशेष नाम दिया जा सकता है?
समांतर चतुर्भुज ABCD के विकर्ण, AC पर बिंदु E और F इस प्रकार स्थित हैं कि AE = CF है। दर्शाइए कि BFDE एक समांतर चतुर्भुज है।
निम्न में से कौन एक समांतर चतुर्भुज का गुण है?
किसी समांतर चतुर्भुज के एक अधिक कोण वाले शीर्ष से खींचे गये दो शीर्षलंबों के बीच का कोण 30∘ है। उस अधिक कोण की माप है –
एक समांतर चतुर्भुज की रचना कीजिए जिसकी एक भुजा 4 cm और दोनों विकर्ण 5.6 cm और 7 cm हों। दूसरी भुजा को मापिए।
आकृति में `square` ABCD समांतर चतुर्भुज है। किरण AB पर बिंदु E इस प्रकार है कि BE = AB तो सिद्ध कीजिए कि रेखा ED यह रेख BC को बिंदु F पर समद्विभाजित करती है।

