Advertisements
Advertisements
Question
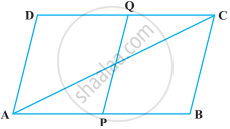
समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति में)। दर्शाइए कि
- यह ∠C को भी समद्विभाजित करता है।
- ABCD एक समचतुर्भुज है
Advertisements
Solution
(i) ABCD एक समांतर चतुर्भुज है।
∴ ∠DAC = ∠BCA ...(एकांतर अंत: कोण) ...(1)
और, ∠BAC = ∠DCA ...(एकांतर अंत: कोण) ...(2)
हालाँकि, यह दिया गया है कि AC, ∠A को समद्विभाजित करता है।
∴ ∠DAC = ∠BAC ...(3)
समीकरण (1), (2) और (3) से, हम प्राप्त करते हैं
∠DAC = ∠BCA = ∠BAC = ∠DCA ...(4)
⇒ ∠DCA = ∠BCA
इसलिए, AC, ∠C को समद्विभाजित करता है।
(ii) समीकरण (4) से, हम प्राप्त करते हैं
∠DAC = ∠DCA
∴ DA = DC ...(बराबर कोणों के सम्मुख भुजाएँ बराबर होती हैं।)
हालाँकि, DA = BC और AB = CD ...(समानांतर चतुर्भुज की सम्मुख भुजाएँ)
∴ AB = BC = CD = DA
अतः, ABCD एक समचतुर्भुज है।
APPEARS IN
RELATED QUESTIONS
ABCD एक समांतर चतुर्भुज है। प्रत्येक कथन को परिभाषा या प्रयोग किए गए गुण द्वारा पूरा कीजिए :
- AD = ______
- ∠DCB = ______
- OC = ______
- m∠DAB + m∠CDA = ______
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠A = 70° और ∠C = 65°?
ABCD एक समचतुर्भुज है, जिसमें D से AB पर शीर्षलंब AB को समद्विभाजित करता है। समचतुर्भुज के कोण ज्ञात कीजिए।
E एक समलंब ABCD की भुजा AD का मध्य-बिंदु है, जिसमें AB || DC है। E से होकर AB के समांतर खींची गई रेखा BC को F पर प्रतिच्छेद करती है। दर्शाइए कि F भुजा BC का मध्य-बिंदु है। [संकेत : AC को मिलाइए]
समांतर चतुर्भुज LOST में, SN ⊥ OL और SM ⊥ LT है। ∠STM, ∠SON और ∠NSM ज्ञात कीजिए।
ABCD एक समांतर चतुर्भुज है। x, y और z के मान ज्ञात कीजिए।
किसी समांतर चतुर्भुज का एक विकर्ण उसके एक कोण को समद्विभाजित करता है। क्या वह दूसरे कोण को भी समद्विभाजित करेगा? कारण दीजिए।
निम्न आकृति में, FD || BC || AE है और AC || ED है। x का मान ज्ञात कीजिए –
आकृति में `square` ABCD समांतर चतुर्भुज है। किरण AB पर बिंदु E इस प्रकार है कि BE = AB तो सिद्ध कीजिए कि रेखा ED यह रेख BC को बिंदु F पर समद्विभाजित करती है।
संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR
