Advertisements
Advertisements
Question
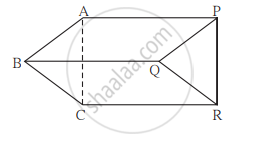
संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR
Solution
दत्त: रेख AB || रेख PQ , रेख AB ≅ रेख PQ,
रेख AC || रेख PR, रेख AC ≅ रेख PR
साध्य: रेख BC || रेख QR तथा रेख BC ≅ रेख QR
उपपत्ति:
`square` ABQP में,
रेख AB || रेख PQ
रेख AB ≅ रेख PQ ...(दत्त)
∴ `square` ABQP एक समांतर चतुर्भुज है। ...(यदि किसी चतुर्भुज की सम्मुख भुजा सर्वांगसम तथा समांतर हो, तो वह समांतर होता है।)
∴ रेख AP || रेख BQ ...(i)
∴ रेख AP ≅ रेख BQ ...(ii) ...(समांतर चतुर्भुज की सम्मुख भुजाएँ)
`square` ACRP में,
रेख AC || रेख PR
रेख AC ≅ रेख PR ...(दत्त)
∴ `square` ACRP एक समांतर चतुर्भुज है। ...(यदि किसी चतुर्भुज की सम्मुख भुजा सर्वांगसम तथा समांतर हो, तो वह समांतर होता है।)
∴ रेख AP || रेख CR ...(iii)
∴ रेख AP ≅ रेख CR ...(iv) ...(समांतर चतुर्भुज की सम्मुख भुजाएँ)
`square` BQRC में,
रेख BQ || रेख CR ...[(i) तथा (iii) से]
रेख BQ ≅ रेख CR ...[(ii) तथा (iv) से]
∴ `square` BQRC एक समांतर चतुर्भुज है। ...(यदि किसी चतुर्भुज की सम्मुख भुजा सर्वांगसम तथा समांतर हो, तो वह समांतर होता है।)
∴ रेख BC || रेख QR
∴ रेख BC ≅ रेख QR ...(समांतर चतुर्भुज की सम्मुख भुजाएँ)
APPEARS IN
RELATED QUESTIONS
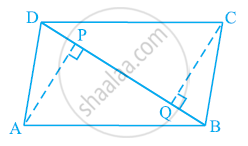
ABCD एक समांतर चतुर्भज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं (देखिए आकृति में)। दर्शाइए कि
- ΔAPB ≅ ΔCQD
- AP = CQ
निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए :

एक समांतर चतुर्भुज ABCD में, AB = 10 cm और AD = 6 cm है। ∠A का समद्विभाजक DC से E पर मिलता है तथा AE और BC बढ़ाने पर F पर मिलते हैं। CF की लंबाई ज्ञात कीजिए।
नीचे दी गयी आकृतियों में से कौन-सी आकृति निम्नलिखित गुणों को संतुष्ट करती है?
- सभी भुजाएँ बराबर हैं।
- सभी कोण समकोण हैं।
- सम्मुख भुजाएँ समांतर हैं।
किसी समांतर चतुर्भुज के एक अधिक कोण वाले शीर्ष से खींचे गये दो शीर्षलंबों के बीच का कोण 30∘ है। उस अधिक कोण की माप है –
एक समांतर चतुर्भुज की रचना कीजिए जिसकी एक भुजा 4 cm और दोनों विकर्ण 5.6 cm और 7 cm हों। दूसरी भुजा को मापिए।
आकृति में `square` PQRS तथा `square` ABCR दो समांतर चतुर्भुज है। ∠P = 110° तो `square `ABCR के सभी कोणों के माप ज्ञात कीजिए।

आकृति में `square` ABCD समांतर चतुर्भुज है। किरण AB पर बिंदु E इस प्रकार है कि BE = AB तो सिद्ध कीजिए कि रेखा ED यह रेख BC को बिंदु F पर समद्विभाजित करती है।

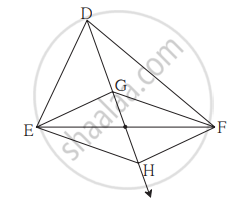
आकृति में, बिंदु G, ΔDEF की माध्यिकाओं का संगामी बिंदु है। किरण DG पर बिंदु H इस प्रकार लें कि D-G-H तथा DG = GH, हो तो सिद्ध कीजिए कि `square` GEHF समांतर चतुर्भुज है।
समांतर चतुर्भुज की दो संलग्न भुजाओं का अनुपात 3 : 4 है। उसकी परिमिति 112 सेमी हो तो उसकी प्रत्येक भुजा की लंबाई ज्ञात कीजिए।
