Advertisements
Advertisements
Question
ABCD एक समांतर चतुर्भुज है। भुजा AB और AD पर क्रमशः बिंदु P और Q इस प्रकार लिये गये हैं कि एक समांतर चतुर्भुज PRQA बनता है। यदि ∠C = 45∘ है, तो ∠R ज्ञात कीजिए।
Solution
माना ABCD एक समांतर चतुर्भुज है,
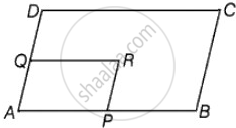
दिया गया है: ∠C = 45°
एक समांतर चतुर्भुज ABCD में,
∠A = ∠C ...[समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।]
इसी प्रकार, समान्तर चतुर्भुज PRQA में,
∠A = ∠R ...[समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।]
अतः, ∠R = 45°
APPEARS IN
RELATED QUESTIONS
यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
किसी समांतर चतुर्भुज के दो आसन्न कोणों का अनुपात 3 : 2 है। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
एक चतुर्भुज का नाम बताइए जिसके विकर्ण एक दूसरे को समद्विभाजित करते है।
एक समांतर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर प्रतिच्छेद करते हैं। यदि OA = 3 cm और OD = 2 cm है, तो AC और BD की लंबाई ज्ञात कीजिए।
निम्नलिखित आकृति में, ABCD और AEFG दो समांतर चतुर्भुज हैं यदि ∠C = 55° है, तो ∠F निर्धारित कीजिए।
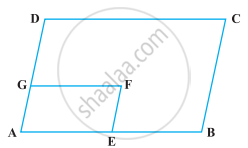
क्या किसी चतुर्भुज के सभी कोण न्यून कोण हो सकते हैं? अपने उत्तर का कारण दीजिए।
ABCD एक समचतुर्भुज है, जिसमें D से AB पर शीर्षलंब AB को समद्विभाजित करता है। समचतुर्भुज के कोण ज्ञात कीजिए।
नीचे दी गयी आकृतियों में से कौन-सी आकृति निम्नलिखित गुणों को संतुष्ट करती है?
- सभी भुजाएँ बराबर हैं।
- सभी कोण समकोण हैं।
- सम्मुख भुजाएँ समांतर हैं।
निम्न में से कौन एक समांतर चतुर्भुज का गुण है?
नीचे दिये समांतर चतुर्भुज PQRS में, O विकर्ण SQ का मध्य बिंदु है। ∠S, ∠R, PQ, QR और विकर्ण PR ज्ञात कीजिए।
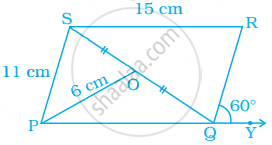
एक समांतर चतुर्भुज MODE में, ∠M कोण ∠O के समद्विभाजक Q पर मिलते हैं। ∠MQO की माप ज्ञात कीजिए।
एक समांतर चतुर्भुज के अधिक कोण वाले शीर्ष से खींचे गये दो शीर्षलंबों के बीच का कोण 45∘ है। इस समांतर चतुर्भुज के कोण ज्ञात कीजिए।
निम्न आकृति में, FD || BC || AE है और AC || ED है। x का मान ज्ञात कीजिए –
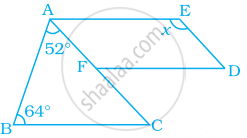
एक समांतर चतुर्भुज HOME की रचना कीजिए, जिसमें HO = 6 cm, HE = 4 cm और OE = 3 cm है।
आकृति में `square` PQRS तथा `square` ABCR दो समांतर चतुर्भुज है। ∠P = 110° तो `square `ABCR के सभी कोणों के माप ज्ञात कीजिए।

आकृति में `square` ABCD समांतर चतुर्भुज है। किरण AB पर बिंदु E इस प्रकार है कि BE = AB तो सिद्ध कीजिए कि रेखा ED यह रेख BC को बिंदु F पर समद्विभाजित करती है।

संलग्न आकृति में समांतर चतुर्भुज `square` ABCD की भुजाओं पर P, Q, R, S इस प्रकार है कि, AP = BQ = CR = DS तो सिद्ध कीजिए कि `square` PQRS समांतर चतुर्भुज है।

