Advertisements
Advertisements
Question
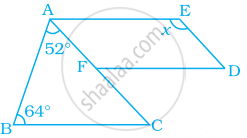
निम्न आकृति में, FD || BC || AE है और AC || ED है। x का मान ज्ञात कीजिए –
Solution
दिया गया है: FD || BC || AE और AC || ED।
निर्माण: DF को इस प्रकार बढ़ाइए कि वह AB को G पर प्रतिच्छेद करे।
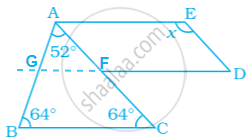
त्रिभुज ABC में,
∠A + ∠B + ∠C = 180° ...[त्रिभुज के कोणों के योग का गुण]
52° + 64° + ∠C = 180°
∠C = 180° – (52° + 64°)
∠C = 180° – 116°
∠C = 64°
अब, जैसा कि देखा जा सकता है कि DG || BC और DG || AE,
∠ACB = ∠AFG ...[FG || BC और FC एक तिर्यक रेखा है, इसलिए, संगत कोण]
64° = ∠AFG
साथ ही, GFD एक सीधी रेखा है।
तो, ∠GFA + ∠AFD = 180° ...[रैखिक युग्म]
64° + ∠AFD = 180°
∠AFD = 180° – 64°
∠AFD = 116°
साथ ही, FD || AE और AF || ED
अतः, AEDF एक समांतर चतुर्भुज है।
अब, ∠AFD = ∠AEF ...[समांतर चतुर्भुज में सम्मुख कोण बराबर होते हैं।]
∠AED = x = 116°
APPEARS IN
RELATED QUESTIONS
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि:
- ABCD एक वर्ग है।
- विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
ABCD एक समांतर चतुर्भज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं (देखिए आकृति में)। दर्शाइए कि
- ΔAPB ≅ ΔCQD
- AP = CQ
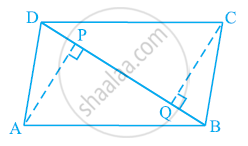
ABCD एक समलंब है, जिसमें AB || DC और AD = BC है (देखिए आकृति में)। दर्शाइए कि
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- विकर्ण AC = विकर्ण BD है।
[संकेत: AB को बढ़ाइए और C से होकर DA के समांतर एक रेखा खींचिए जो बढ़ी हुई भुजा AB को E पर प्रतिच्छेद करे।]
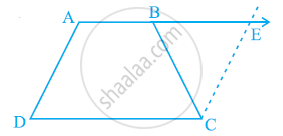
निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:
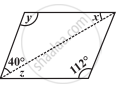
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि AB = DC = 8 cm, AD = 4 cm और BC = 4.4 cm?
किसी समांतर चतुर्भुज के दो आसन्न कोणों का अनुपात 3 : 2 है। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
∆ABC में, AB = 5 cm, BC = 8 cm और CA = 7 cm हैं। यदि D और E क्रमश : AB और BC के मध्य-बिंदु हैं, तो DE की लंबाई निर्धारित कीजिए।
एक चतुर्भुज ABCD के सम्मुख कोण बराबर हैं। यदि AB = 4 cm है, तो CD निर्धारित कीजिए।
समांतर चतुर्भुज ABCD के विकर्ण, AC पर बिंदु E और F इस प्रकार स्थित हैं कि AE = CF है। दर्शाइए कि BFDE एक समांतर चतुर्भुज है।
E एक समलंब ABCD की भुजा AD का मध्य-बिंदु है, जिसमें AB || DC है। E से होकर AB के समांतर खींची गई रेखा BC को F पर प्रतिच्छेद करती है। दर्शाइए कि F भुजा BC का मध्य-बिंदु है। [संकेत : AC को मिलाइए]
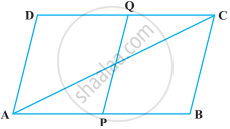
एक समांतर चतुर्भुज ABCD की सम्मुख भुजाओं AB और CD पर क्रमश : बिंदु P और Q इस प्रकार लिए गए हैं कि AP = CQ है। (आकृति)। दर्शाइए कि AC और PQ परस्पर समद्विभाजित करते हैं।
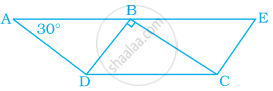
नीचे दी गयी आकृति में, ABCD और BDCE एक ही आधार DC पर दो समांतर चतुर्भुज हैं। यदि BC ⊥ BD है, तो ∠BEC बराबर है –
सभी आयत समांतर चतुर्भुज होते हैं।
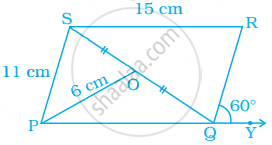
नीचे दिये समांतर चतुर्भुज PQRS में, O विकर्ण SQ का मध्य बिंदु है। ∠S, ∠R, PQ, QR और विकर्ण PR ज्ञात कीजिए।
एक समांतर चतुर्भुज MODE में, ∠M कोण ∠O के समद्विभाजक Q पर मिलते हैं। ∠MQO की माप ज्ञात कीजिए।
किसी चतुर्भुज के दो कोणों में से प्रत्येक की माप 75∘ है तथा अन्य दो कोण बराबर हैं। इन दोनों कोणों के माप क्या हैं? संभावित बनने वाली आकृतियों के नाम लिखिए।
ABCD एक समांतर चतुर्भुज है। भुजा AB और AD पर क्रमशः बिंदु P और Q इस प्रकार लिये गये हैं कि एक समांतर चतुर्भुज PRQA बनता है। यदि ∠C = 45∘ है, तो ∠R ज्ञात कीजिए।
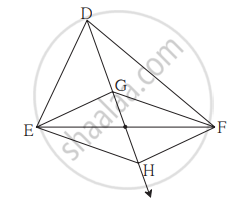
आकृति में, बिंदु G, ΔDEF की माध्यिकाओं का संगामी बिंदु है। किरण DG पर बिंदु H इस प्रकार लें कि D-G-H तथा DG = GH, हो तो सिद्ध कीजिए कि `square` GEHF समांतर चतुर्भुज है।