Advertisements
Advertisements
Question
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि:
- ABCD एक वर्ग है।
- विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
Solution
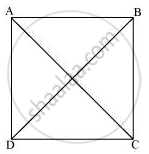
(i) यह दिया गया है कि ABCD एक आयत है।
∴ ∠A = ∠C
⇒ `1/2∠"A" = 1/2∠"C"`
⇒ ∠DAC = ∠DCA ...(AC, ∠A तथा ∠C को समद्विभाजित करता है।)
CD = DA ...(बराबर कोणों के सम्मुख भुजाएँ भी बराबर होती हैं।)
हालाँकि, DA = BC और AB = CD ...(एक आयत की सम्मुख भुजाएँ बराबर होती हैं।)
∴ AB = BC = CD = DA
ABCD एक आयत है और इसकी सभी भुजाएँ बराबर हैं।
अतः, ABCD एक वर्ग है।
(ii) आइए BD को जोड़ें।
ΔBCD में,
BC = CD ...(एक वर्ग की भुजाएँ एक दूसरे के बराबर होती हैं।)
∠CDB = ∠CBD ...(बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।)
हालाँकि, ∠CDB = ∠ABD ...(AB || CD के लिए एकांतर अंतः कोण)
∴ ∠CBD = ∠ABD
⇒ BD, ∠B को समद्विभाजित करता है।
साथ ही, ∠CBD = ∠ADB ...(BC || AD के लिए एकांतर अंतः कोण)
⇒ ∠CDB = ∠ABD
∴ BD, ∠D को समद्विभाजित करता है।
APPEARS IN
RELATED QUESTIONS
यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति में)। दर्शाइए कि
- यह ∠C को भी समद्विभाजित करता है।
- ABCD एक समचतुर्भुज है

ABCD एक समांतर चतुर्भुज है। प्रत्येक कथन को परिभाषा या प्रयोग किए गए गुण द्वारा पूरा कीजिए :

- AD = ______
- ∠DCB = ______
- OC = ______
- m∠DAB + m∠CDA = ______
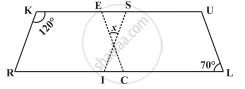
दी गई आकृति में RISK तथा CLUE दोनों समांतर चतुर्भुज हैं, x का मान ज्ञात कीजिए।
समांतर चतुर्भुज ABCD के विकर्ण, AC पर बिंदु E और F इस प्रकार स्थित हैं कि AE = CF है। दर्शाइए कि BFDE एक समांतर चतुर्भुज है।
निम्न में से कौन एक समांतर चतुर्भुज का गुण है?
यदि किसी समांतर चतुर्भुज के दो आसन्न कोण (5x − 5)∘ और (10x + 35)∘ हैं, तो इन कोणों का अनुपात होगा –
समांतर ABCD में, ∠A का समद्विभाजक BC को समद्विभाजित करता है। क्या कोण B का समद्विभाजक AD को भी समद्विभाजित करता है? कारण दीजिए।
एक समांतर चतुर्भुज ABCD की रचना कीजिए, जिसमें AB = 4cm, BC = 5 cm और ∠B = 60∘ है।
एक समांतर चतुर्भुज HOME की रचना कीजिए, जिसमें HO = 6 cm, HE = 4 cm और OE = 3 cm है।
