Advertisements
Advertisements
Question
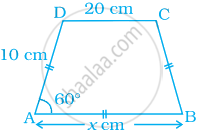
निम्न आकृति में, AB || DC और AD = BC है। x का मान ज्ञात कीजिए –
Solution
दिया गया है: एक समद्विबाहु समलंब, AB || DC, AD = BC और ∠A = 60°।
तो, ∠B = 60°।
निर्माण: D से होकर BC के समांतर एक रेखा खींचिए।
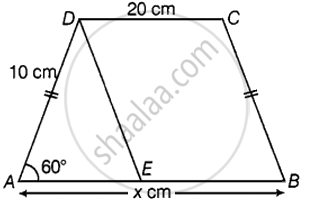
अब, DEBC एक समांतर चतुर्भुज है,
BE = CD = 20 सेमी और DE = BC = 10 सेमी है।
अब, ∠DEB + ∠CBE = 180° ...[समांतर चतुर्भुज में आसन्न कोण संपूरक होते हैं।]
∠DEB = 180° – 60°
∠DEB = 120°
त्रिभुज ADE में,
∠ADE = 60° ...[बाहरी कोण]
साथ ही, त्रिभुज ADE एक समबाहु त्रिभुज है।
AE = 10 cm
AB = AE + EB
AB = 10 + 20
AB = 30 cm
अत:, x = 30 सेमी।
APPEARS IN
RELATED QUESTIONS
आकृति में m∠C ज्ञात कीजिए जदि `overline("AB") || overline("DC")` है।

निम्नलिखित गुणों में से किस एक के द्वारा एक समलंब की व्याख्या होती है?
एक समलंब ABCD, जिसमें AB || CD है, यदि ∠A = 100∘ है, तो ∠D = ______ होगा।
समलंब के सभी कोण बराबर होते हैं।
प्रत्येक समलंब एक आयत है।
प्रत्येक समचतुर्भुज एक समलंब है।
चार चतुर्भुजों - वर्ग, आयत, समचतुर्भुज और समलंब में से एक अन्य तीन से अपने डिजाइन के कारण कुछ भिन्न हैं। उसे ज्ञात कीजिए और उसका औचित्य दीजिए।
एक समलंब ABCD की रचना कीजिए, जिसमें AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm और CD = 9.6 cm है। ∠B और ∠A को मापिए।
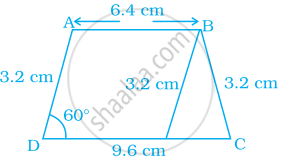
[सिंकेत – दोनों समांतर भुजाओं के अंतर से एक समबाहु त्रिभुज की भुजा प्राप्त होती है।]
यदि `square` IJKL में भुजा IJ || भुजा KL हो और `angle`I = 108° `angle`K = 53° तो `angle`J तथा `angle`L के माप ज्ञात कीजिए।
आकृति में `square`ABCD में भुजा BC < भुजा AD, भुजा BC || भुजा AD तथा यदि भुजा BA ≅ भुजा CD हो तो सिद्ध कीजिए कि `angle`ABC ≅ `angle`DCB