Advertisements
Advertisements
Question
एक समलंब ABCD की रचना कीजिए, जिसमें AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm और CD = 9.6 cm है। ∠B और ∠A को मापिए।
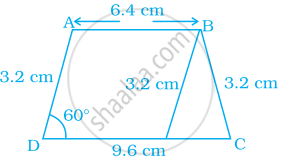
[सिंकेत – दोनों समांतर भुजाओं के अंतर से एक समबाहु त्रिभुज की भुजा प्राप्त होती है।]
Solution
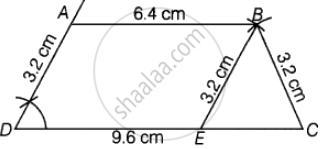
रचना के चरण -
चरण I - रेखाखंड DC = 9.6 सेमी खींचिए।
चरण II - D को केंद्र मानकर 60 का कोण बनाएं। अब, इसे 3.2 सेमी के चाप से काटें जिसे बिंदु A कहते हैं।
चरण III - अब, एक समांतर AB || CD खींचिए।
चरण IV - C को केंद्र मानकर, पिछली समांतर रेखा पर 3.2 सेमी माप का एक चाप B काटें।
चरण V - चाप B से एक रेखाखंड BE = 3.2 सेमी खींचिए।
चरण VI - B को E और C से जोड़ें।
अतः, ABCD अभीष्ट समलम्ब है, जहाँ ∠A = 120° और ∠B = 60° है।
APPEARS IN
RELATED QUESTIONS
आकृति में m∠C ज्ञात कीजिए जदि `overline("AB") || overline("DC")` है।

सभी वर्ग समलंब होते है।
उन सभी चतुर्भुजों की पहचान कीजिए जिनमें चारों भुजाएँ बराबर लंबाई की हो।
निम्न में से कौन-सी आकृति नीचे लिखे गुण को संतुष्ट करती है?
“भुजाओं का केवल एक युग्म समांतर है।”
निम्न में से कौन-सी आकृति नीचे लिखे गुणों में से किसी भी गुण को संतुष्ट नहीं करती?
"सभी भुजाएँ बराबर हैं।"
"सभी कोण समकोण हैं।"
"सम्मुख भुजाएँ समान्तर हैं।"
समलंब के सभी कोण बराबर होते हैं।
चार चतुर्भुजों - वर्ग, आयत, समचतुर्भुज और समलंब में से एक अन्य तीन से अपने डिजाइन के कारण कुछ भिन्न हैं। उसे ज्ञात कीजिए और उसका औचित्य दीजिए।
ABCD एक समलंब है, जिसमें AB || CD, ∠A : ∠D = 2 : 1 और ∠B : ∠C = 7 : 5 है। इस समलंब के कोण ज्ञात कीजिए।
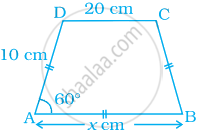
निम्न आकृति में, AB || DC और AD = BC है। x का मान ज्ञात कीजिए –
यदि `square` IJKL में भुजा IJ || भुजा KL हो और `angle`I = 108° `angle`K = 53° तो `angle`J तथा `angle`L के माप ज्ञात कीजिए।
