Advertisements
Advertisements
प्रश्न
एक समलंब ABCD की रचना कीजिए, जिसमें AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm और CD = 9.6 cm है। ∠B और ∠A को मापिए।
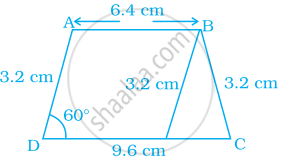
[सिंकेत – दोनों समांतर भुजाओं के अंतर से एक समबाहु त्रिभुज की भुजा प्राप्त होती है।]
उत्तर
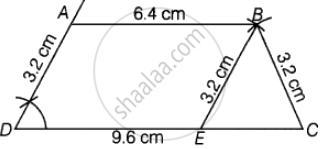
रचना के चरण -
चरण I - रेखाखंड DC = 9.6 सेमी खींचिए।
चरण II - D को केंद्र मानकर 60 का कोण बनाएं। अब, इसे 3.2 सेमी के चाप से काटें जिसे बिंदु A कहते हैं।
चरण III - अब, एक समांतर AB || CD खींचिए।
चरण IV - C को केंद्र मानकर, पिछली समांतर रेखा पर 3.2 सेमी माप का एक चाप B काटें।
चरण V - चाप B से एक रेखाखंड BE = 3.2 सेमी खींचिए।
चरण VI - B को E और C से जोड़ें।
अतः, ABCD अभीष्ट समलम्ब है, जहाँ ∠A = 120° और ∠B = 60° है।
APPEARS IN
संबंधित प्रश्न
सभी समांतर चतुर्भुज समलंब होते है।
सभी वर्ग समलंब होते है।
PQRS एक समलंब है, जिसमें PQ || SR है तथा ∠P = 130∘ और ∠Q = 110∘ है। तब ∠R बराबर है –
एक समलंब ABCD, जिसमें AB || CD है, यदि ∠A = 100∘ है, तो ∠D = ______ होगा।
प्रत्येक समलंब एक समांतर चतुर्भुज है।
समलंब HARE में, EP और RP क्रमश: ∠E और ∠R के समद्विभाजक हैं। ∠HAR और ∠EHA ज्ञात कीजिए।

एक चतुर्भुज HOPE में, PS और ES क्रमशः ∠P और ∠E के समद्विभाजक हैं। क्या ∠O + ∠H = 2∠PSE है? कारण दीजिए।
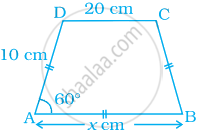
निम्न आकृति में, AB || DC और AD = BC है। x का मान ज्ञात कीजिए –
एक समलंब RISK की रचना कीजिए, जिसमें RI ।। KS, RI = 7 cm, IS = 5 cm, RK = 6.5 cm और ∠I = 60∘ है।
`square` ABCD में भुजा BC || भुजा AD, हो और भुजा AB ≅ भुजा DC, `angle`A = 72° तो `angle`B, तथा `angle`D के माप निश्चित कीजिए।
