Advertisements
Advertisements
प्रश्न
एक समलंब ABCD की रचना कीजिए, जिसमें AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm और CD = 9.6 cm है। ∠B और ∠A को मापिए।
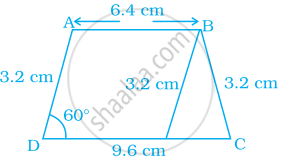
[सिंकेत – दोनों समांतर भुजाओं के अंतर से एक समबाहु त्रिभुज की भुजा प्राप्त होती है।]
उत्तर
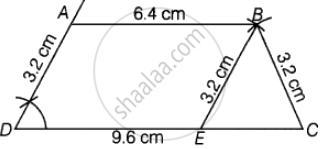
रचना के चरण -
चरण I - रेखाखंड DC = 9.6 सेमी खींचिए।
चरण II - D को केंद्र मानकर 60 का कोण बनाएं। अब, इसे 3.2 सेमी के चाप से काटें जिसे बिंदु A कहते हैं।
चरण III - अब, एक समांतर AB || CD खींचिए।
चरण IV - C को केंद्र मानकर, पिछली समांतर रेखा पर 3.2 सेमी माप का एक चाप B काटें।
चरण V - चाप B से एक रेखाखंड BE = 3.2 सेमी खींचिए।
चरण VI - B को E और C से जोड़ें।
अतः, ABCD अभीष्ट समलम्ब है, जहाँ ∠A = 120° और ∠B = 60° है।
APPEARS IN
संबंधित प्रश्न
सभी वर्ग समलंब होते है।
उन सभी चतुर्भुजों की पहचान कीजिए जिनमें चारों भुजाएँ बराबर लंबाई की हो।
निम्न में से कौन-सी आकृति नीचे लिखे गुणों में से किसी भी गुण को संतुष्ट नहीं करती?
"सभी भुजाएँ बराबर हैं।"
"सभी कोण समकोण हैं।"
"सम्मुख भुजाएँ समान्तर हैं।"
प्रत्येक समलंब एक आयत है।
एक चतुर्भुज HOPE में, PS और ES क्रमशः ∠P और ∠E के समद्विभाजक हैं। क्या ∠O + ∠H = 2∠PSE है? कारण दीजिए।
ABCD एक समलंब है, जिसमें AB || CD, ∠A : ∠D = 2 : 1 और ∠B : ∠C = 7 : 5 है। इस समलंब के कोण ज्ञात कीजिए।
एक समलंब ABCD की रचना कीजिए, जिसमें AB || DC, ∠A = 105∘, AD = 3 cm, AB = 4 cm और CD = 8 cm है।
एक समलंब RISK की रचना कीजिए, जिसमें RI ।। KS, RI = 7 cm, IS = 5 cm, RK = 6.5 cm और ∠I = 60∘ है।
यदि `square` IJKL में भुजा IJ || भुजा KL हो और `angle`I = 108° `angle`K = 53° तो `angle`J तथा `angle`L के माप ज्ञात कीजिए।
आकृति में `square`ABCD में भुजा BC < भुजा AD, भुजा BC || भुजा AD तथा यदि भुजा BA ≅ भुजा CD हो तो सिद्ध कीजिए कि `angle`ABC ≅ `angle`DCB