Advertisements
Advertisements
प्रश्न
एक चतुर्भुज HOPE में, PS और ES क्रमशः ∠P और ∠E के समद्विभाजक हैं। क्या ∠O + ∠H = 2∠PSE है? कारण दीजिए।
उत्तर
∠SHO = ∠SHE = ∠1
∠HES = ∠SEP = ∠2
ΔSHE
∠1 + ∠2 + ∠PSE = 180°
∠H + ∠O + ∠P + ∠E = 360°
2∠1 + ∠O + ∠P + 2∠2 = 360°
2(∠1 + ∠2) + ∠O + ∠P = 360°
2(180° − ∠PSE) + ∠O + ∠P = 360°
360° − 2∠PSE + ∠O + ∠P = 360°
∠O + ∠P = 2∠PSE
APPEARS IN
संबंधित प्रश्न
सभी वर्ग समलंब होते है।
उन सभी चतुर्भुजों की पहचान कीजिए जिनमें चारों भुजाएँ बराबर लंबाई की हो।
PQRS एक समलंब है, जिसमें PQ || SR है तथा ∠P = 130∘ और ∠Q = 110∘ है। तब ∠R बराबर है –
एक समलंब ABCD, जिसमें AB || CD है, यदि ∠A = 100∘ है, तो ∠D = ______ होगा।
समलंब के सभी कोण बराबर होते हैं।
प्रत्येक समलंब एक समांतर चतुर्भुज है।
चार चतुर्भुजों - वर्ग, आयत, समचतुर्भुज और समलंब में से एक अन्य तीन से अपने डिजाइन के कारण कुछ भिन्न हैं। उसे ज्ञात कीजिए और उसका औचित्य दीजिए।
एक समलंब ABCD की रचना कीजिए, जिसमें AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm और CD = 9.6 cm है। ∠B और ∠A को मापिए।
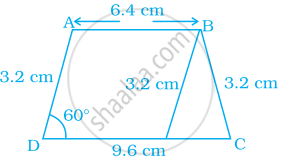
[सिंकेत – दोनों समांतर भुजाओं के अंतर से एक समबाहु त्रिभुज की भुजा प्राप्त होती है।]
यदि `square` IJKL में भुजा IJ || भुजा KL हो और `angle`I = 108° `angle`K = 53° तो `angle`J तथा `angle`L के माप ज्ञात कीजिए।
आकृति में `square`ABCD में भुजा BC < भुजा AD, भुजा BC || भुजा AD तथा यदि भुजा BA ≅ भुजा CD हो तो सिद्ध कीजिए कि `angle`ABC ≅ `angle`DCB