Advertisements
Advertisements
Question
एक चतुर्भुज HOPE में, PS और ES क्रमशः ∠P और ∠E के समद्विभाजक हैं। क्या ∠O + ∠H = 2∠PSE है? कारण दीजिए।
Solution
∠SHO = ∠SHE = ∠1
∠HES = ∠SEP = ∠2
ΔSHE
∠1 + ∠2 + ∠PSE = 180°
∠H + ∠O + ∠P + ∠E = 360°
2∠1 + ∠O + ∠P + 2∠2 = 360°
2(∠1 + ∠2) + ∠O + ∠P = 360°
2(180° − ∠PSE) + ∠O + ∠P = 360°
360° − 2∠PSE + ∠O + ∠P = 360°
∠O + ∠P = 2∠PSE
APPEARS IN
RELATED QUESTIONS
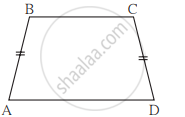
आकृति में m∠C ज्ञात कीजिए जदि `overline("AB") || overline("DC")` है।

सभी समांतर चतुर्भुज समलंब होते है।
एक चतुर्भुज, जिसमें सम्मुख भुजाओं का एक युग्म समांतर हो, ______ कहलाता है।
प्रत्येक समचतुर्भुज एक समलंब है।
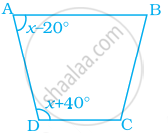
नीचे दिये गये समलंब ABCD में, x का मान ज्ञात कीजिए –
ABCD एक समलंब है, जिसमें AB || CD, ∠A : ∠D = 2 : 1 और ∠B : ∠C = 7 : 5 है। इस समलंब के कोण ज्ञात कीजिए।
एक समलंब ABCD की रचना कीजिए, जिसमें AB || DC, ∠A = 105∘, AD = 3 cm, AB = 4 cm और CD = 8 cm है।
एक समलंब RISK की रचना कीजिए, जिसमें RI ।। KS, RI = 7 cm, IS = 5 cm, RK = 6.5 cm और ∠I = 60∘ है।
`square` ABCD में भुजा BC || भुजा AD, हो और भुजा AB ≅ भुजा DC, `angle`A = 72° तो `angle`B, तथा `angle`D के माप निश्चित कीजिए।
आकृति में `square`ABCD में भुजा BC < भुजा AD, भुजा BC || भुजा AD तथा यदि भुजा BA ≅ भुजा CD हो तो सिद्ध कीजिए कि `angle`ABC ≅ `angle`DCB