Advertisements
Advertisements
प्रश्न
एक चतुर्भुज HOPE में, PS और ES क्रमशः ∠P और ∠E के समद्विभाजक हैं। क्या ∠O + ∠H = 2∠PSE है? कारण दीजिए।
उत्तर
∠SHO = ∠SHE = ∠1
∠HES = ∠SEP = ∠2
ΔSHE
∠1 + ∠2 + ∠PSE = 180°
∠H + ∠O + ∠P + ∠E = 360°
2∠1 + ∠O + ∠P + 2∠2 = 360°
2(∠1 + ∠2) + ∠O + ∠P = 360°
2(180° − ∠PSE) + ∠O + ∠P = 360°
360° − 2∠PSE + ∠O + ∠P = 360°
∠O + ∠P = 2∠PSE
APPEARS IN
संबंधित प्रश्न
सभी वर्ग समलंब होते है।
उन सभी चतुर्भुजों की पहचान कीजिए जिनमें चारों भुजाएँ बराबर लंबाई की हो।
निम्न में से कौन-सी आकृति नीचे लिखे गुण को संतुष्ट करती है?
“भुजाओं का केवल एक युग्म समांतर है।”
निम्नलिखित गुणों में से किस एक के द्वारा एक समलंब की व्याख्या होती है?
PQRS एक समलंब है, जिसमें PQ || SR है तथा ∠P = 130∘ और ∠Q = 110∘ है। तब ∠R बराबर है –
चार चतुर्भुजों - वर्ग, आयत, समचतुर्भुज और समलंब में से एक अन्य तीन से अपने डिजाइन के कारण कुछ भिन्न हैं। उसे ज्ञात कीजिए और उसका औचित्य दीजिए।
ABCD एक समलंब है, जिसमें AB || CD, ∠A : ∠D = 2 : 1 और ∠B : ∠C = 7 : 5 है। इस समलंब के कोण ज्ञात कीजिए।
निम्न आकृति में, AB || DC और AD = BC है। x का मान ज्ञात कीजिए –
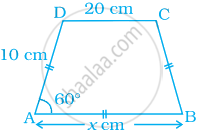
एक समलंब ABCD की रचना कीजिए, जिसमें AB || DC, ∠A = 105∘, AD = 3 cm, AB = 4 cm और CD = 8 cm है।
आकृति में `square`ABCD में भुजा BC < भुजा AD, भुजा BC || भुजा AD तथा यदि भुजा BA ≅ भुजा CD हो तो सिद्ध कीजिए कि `angle`ABC ≅ `angle`DCB