Advertisements
Advertisements
प्रश्न
चार चतुर्भुजों - वर्ग, आयत, समचतुर्भुज और समलंब में से एक अन्य तीन से अपने डिजाइन के कारण कुछ भिन्न हैं। उसे ज्ञात कीजिए और उसका औचित्य दीजिए।
उत्तर
वर्ग, आयत और समचतुर्भुज में सम्मुख भुजाएँ समान्तर और समान होती हैं। साथ ही, सम्मुख कोण बराबर होते हैं, अर्थात वे सभी समांतर चतुर्भुज होते हैं।
लेकिन समलंब में, समानांतर भुजाओं का केवल एक युग्म होता है, अर्थात यह समांतर चतुर्भुज नहीं होता है। इसलिए, समलंब का अलग डिज़ाइन है।
APPEARS IN
संबंधित प्रश्न
आकृति में m∠C ज्ञात कीजिए जदि `overline("AB") || overline("DC")` है।

सभी वर्ग समलंब होते है।
एक चतुर्भुज, जिसमें सम्मुख भुजाओं का एक युग्म समांतर हो, ______ कहलाता है।
प्रत्येक समचतुर्भुज एक समलंब है।
नीचे दिये गये समलंब ABCD में, x का मान ज्ञात कीजिए –
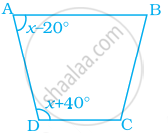
एक चतुर्भुज HOPE में, PS और ES क्रमशः ∠P और ∠E के समद्विभाजक हैं। क्या ∠O + ∠H = 2∠PSE है? कारण दीजिए।
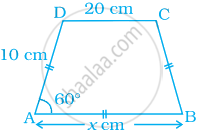
निम्न आकृति में, AB || DC और AD = BC है। x का मान ज्ञात कीजिए –
एक समलंब ABCD की रचना कीजिए, जिसमें AB || DC, ∠A = 105∘, AD = 3 cm, AB = 4 cm और CD = 8 cm है।
एक समलंब ABCD की रचना कीजिए, जिसमें AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm और CD = 9.6 cm है। ∠B और ∠A को मापिए।
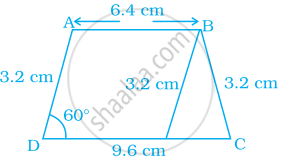
[सिंकेत – दोनों समांतर भुजाओं के अंतर से एक समबाहु त्रिभुज की भुजा प्राप्त होती है।]
`square` ABCD में भुजा BC || भुजा AD, हो और भुजा AB ≅ भुजा DC, `angle`A = 72° तो `angle`B, तथा `angle`D के माप निश्चित कीजिए।
