Advertisements
Advertisements
प्रश्न
एक चतुर्भुज, जिसमें सम्मुख भुजाओं का एक युग्म समांतर हो, ______ कहलाता है।
उत्तर
एक चतुर्भुज, जिसमें सम्मुख भुजाओं का एक युग्म समांतर हो, समलंब कहलाता है।
स्पष्टीकरण -
हम जानते हैं कि, एक समलंब में भुजाओं का एक युग्म समानांतर होता है।
APPEARS IN
संबंधित प्रश्न
निम्न में से कौन-सी आकृति नीचे लिखे गुण को संतुष्ट करती है?
“भुजाओं का केवल एक युग्म समांतर है।”
निम्नलिखित गुणों में से किस एक के द्वारा एक समलंब की व्याख्या होती है?
PQRS एक समलंब है, जिसमें PQ || SR है तथा ∠P = 130∘ और ∠Q = 110∘ है। तब ∠R बराबर है –
प्रत्येक समलंब एक समांतर चतुर्भुज है।
समलंब HARE में, EP और RP क्रमश: ∠E और ∠R के समद्विभाजक हैं। ∠HAR और ∠EHA ज्ञात कीजिए।

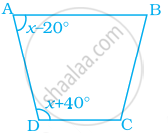
नीचे दिये गये समलंब ABCD में, x का मान ज्ञात कीजिए –
ABCD एक समलंब है, जिसमें AB || CD, ∠A : ∠D = 2 : 1 और ∠B : ∠C = 7 : 5 है। इस समलंब के कोण ज्ञात कीजिए।
एक समलंब RISK की रचना कीजिए, जिसमें RI ।। KS, RI = 7 cm, IS = 5 cm, RK = 6.5 cm और ∠I = 60∘ है।
एक समलंब ABCD की रचना कीजिए, जिसमें AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm और CD = 9.6 cm है। ∠B और ∠A को मापिए।
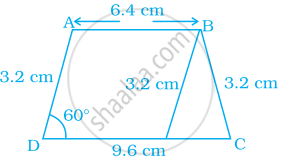
[सिंकेत – दोनों समांतर भुजाओं के अंतर से एक समबाहु त्रिभुज की भुजा प्राप्त होती है।]
आकृति में `square`ABCD में भुजा BC < भुजा AD, भुजा BC || भुजा AD तथा यदि भुजा BA ≅ भुजा CD हो तो सिद्ध कीजिए कि `angle`ABC ≅ `angle`DCB