Advertisements
Advertisements
प्रश्न
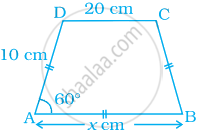
निम्न आकृति में, AB || DC और AD = BC है। x का मान ज्ञात कीजिए –
उत्तर
दिया गया है: एक समद्विबाहु समलंब, AB || DC, AD = BC और ∠A = 60°।
तो, ∠B = 60°।
निर्माण: D से होकर BC के समांतर एक रेखा खींचिए।
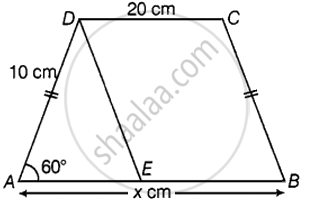
अब, DEBC एक समांतर चतुर्भुज है,
BE = CD = 20 सेमी और DE = BC = 10 सेमी है।
अब, ∠DEB + ∠CBE = 180° ...[समांतर चतुर्भुज में आसन्न कोण संपूरक होते हैं।]
∠DEB = 180° – 60°
∠DEB = 120°
त्रिभुज ADE में,
∠ADE = 60° ...[बाहरी कोण]
साथ ही, त्रिभुज ADE एक समबाहु त्रिभुज है।
AE = 10 cm
AB = AE + EB
AB = 10 + 20
AB = 30 cm
अत:, x = 30 सेमी।
APPEARS IN
संबंधित प्रश्न
सभी समांतर चतुर्भुज समलंब होते है।
निम्न में से कौन-सी आकृति नीचे लिखे गुणों में से किसी भी गुण को संतुष्ट नहीं करती?
"सभी भुजाएँ बराबर हैं।"
"सभी कोण समकोण हैं।"
"सम्मुख भुजाएँ समान्तर हैं।"
एक चतुर्भुज, जिसमें सम्मुख भुजाओं का एक युग्म समांतर हो, ______ कहलाता है।
एक समलंब ABCD, जिसमें AB || CD है, यदि ∠A = 100∘ है, तो ∠D = ______ होगा।
समलंब HARE में, EP और RP क्रमश: ∠E और ∠R के समद्विभाजक हैं। ∠HAR और ∠EHA ज्ञात कीजिए।

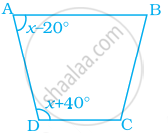
नीचे दिये गये समलंब ABCD में, x का मान ज्ञात कीजिए –
एक समलंब RISK की रचना कीजिए, जिसमें RI ।। KS, RI = 7 cm, IS = 5 cm, RK = 6.5 cm और ∠I = 60∘ है।
एक समलंब ABCD की रचना कीजिए, जिसमें AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm और CD = 9.6 cm है। ∠B और ∠A को मापिए।
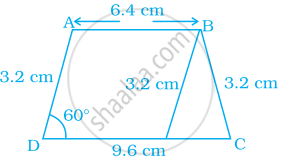
[सिंकेत – दोनों समांतर भुजाओं के अंतर से एक समबाहु त्रिभुज की भुजा प्राप्त होती है।]
`square` ABCD में भुजा BC || भुजा AD, हो और भुजा AB ≅ भुजा DC, `angle`A = 72° तो `angle`B, तथा `angle`D के माप निश्चित कीजिए।
आकृति में `square`ABCD में भुजा BC < भुजा AD, भुजा BC || भुजा AD तथा यदि भुजा BA ≅ भुजा CD हो तो सिद्ध कीजिए कि `angle`ABC ≅ `angle`DCB