Advertisements
Advertisements
प्रश्न
समलंब HARE में, EP और RP क्रमश: ∠E और ∠R के समद्विभाजक हैं। ∠HAR और ∠EHA ज्ञात कीजिए।

उत्तर
क्योंकि EP और PR क्रमशः ∠REH और ∠ARE के कोण समद्विभाजक हैं। ...[दिया गया है।]
चूँकि HARE एक समलंब है,
इसलिए, ∠E + ∠H = 180° और ∠R + ∠A = 180°
⇒ ∠PER + ∠PEH + ∠H = 180° और ∠ERP + ∠PRA + ∠RAH = 180°
⇒ 25° + 25° + ∠H = 180° और 30° + 30° + ∠A = 180°
⇒ 50° + ∠H = 180° और 60° + ∠A = 180°
⇒ ∠H = 130° और ∠A = 120°, अर्थात ∠EHA = 130° और ∠HAR = 120°
APPEARS IN
संबंधित प्रश्न
बताइए कैसे यह आकृति एक समलंब है। इसकी कौन सी दो भुजाएँ समांतर हैं?
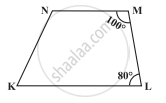
आकृति में m∠C ज्ञात कीजिए जदि `overline("AB") || overline("DC")` है।

उन सभी चतुर्भुजों की पहचान कीजिए जिनमें चारों भुजाएँ बराबर लंबाई की हो।
एक चतुर्भुज, जिसमें सम्मुख भुजाओं का एक युग्म समांतर हो, ______ कहलाता है।
प्रत्येक समलंब एक समांतर चतुर्भुज है।
प्रत्येक समचतुर्भुज एक समलंब है।
एक चतुर्भुज HOPE में, PS और ES क्रमशः ∠P और ∠E के समद्विभाजक हैं। क्या ∠O + ∠H = 2∠PSE है? कारण दीजिए।
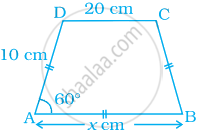
निम्न आकृति में, AB || DC और AD = BC है। x का मान ज्ञात कीजिए –
एक समलंब ABCD की रचना कीजिए, जिसमें AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm और CD = 9.6 cm है। ∠B और ∠A को मापिए।
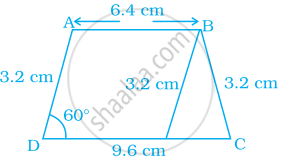
[सिंकेत – दोनों समांतर भुजाओं के अंतर से एक समबाहु त्रिभुज की भुजा प्राप्त होती है।]
`square` ABCD में भुजा BC || भुजा AD, हो और भुजा AB ≅ भुजा DC, `angle`A = 72° तो `angle`B, तथा `angle`D के माप निश्चित कीजिए।
