Advertisements
Advertisements
Question
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि AB = DC = 8 cm, AD = 4 cm और BC = 4.4 cm?
Solution
नहीं, क्योंकि समांतर चतुर्भुज की सम्मुख भुजाएँ समान होती है, परन्तु यहाँ AD ≠ BC है।
APPEARS IN
RELATED QUESTIONS
यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠A = 70° और ∠C = 65°?
किसी समांतर चतुर्भुज के दो आसन्न कोणों का अनुपात 3 : 2 है। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
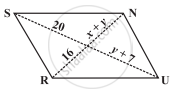
निम्न आकृति RUNS समांतर चतुर्भुज हैं। x तथा y ज्ञात कीजिए (लंबाई cm में है) :
बताइए कैसे एक वर्ग एक समांतर चतुर्भुज है।
निम्नलिखित के लिए कारण दीजिए:
वर्ग एक समांतर चतुर्भुज भी है।
चतुर्भुज ABCD में, ∠A + ∠D = 180° है। इस चतुर्भुज को कौन-सा विशेष नाम दिया जा सकता है?
एक चतुर्भुज ABCD के विकर्ण परस्पर समद्विभाजित करते हैं। यदि ∠A = 35° है, तो ∠B निर्धारित कीजिए।
समांतर चतुर्भुज ABCD के विकर्ण, AC पर बिंदु E और F इस प्रकार स्थित हैं कि AE = CF है। दर्शाइए कि BFDE एक समांतर चतुर्भुज है।
नीचे दी गयी आकृति में, ABCD और BDCE एक ही आधार DC पर दो समांतर चतुर्भुज हैं। यदि BC ⊥ BD है, तो ∠BEC बराबर है –
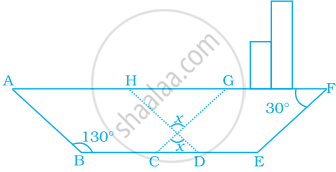
नीचे दिये गये एक जहाज कौँ आकृति में, ABDH और CEFG दो समांतर चतुर्भुज हैं। x का मान ज्ञात कीजिए।
किसी चतुर्भुज के दो कोणों में से प्रत्येक की माप 75∘ है तथा अन्य दो कोण बराबर हैं। इन दोनों कोणों के माप क्या हैं? संभावित बनने वाली आकृतियों के नाम लिखिए।
समांतर ABCD में, ∠A का समद्विभाजक BC को समद्विभाजित करता है। क्या कोण B का समद्विभाजक AD को भी समद्विभाजित करता है? कारण दीजिए।
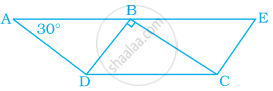
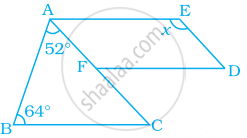
निम्न आकृति में, FD || BC || AE है और AC || ED है। x का मान ज्ञात कीजिए –
एक समांतर चतुर्भुज ABCD की रचना कीजिए, जिसमें AB = 4cm, BC = 5 cm और ∠B = 60∘ है।
एक समांतर चतुर्भुज की रचना कीजिए जिसकी एक भुजा 4 cm और दोनों विकर्ण 5.6 cm और 7 cm हों। दूसरी भुजा को मापिए।
संलग्न आकृति में समांतर चतुर्भुज `square` ABCD की भुजाओं पर P, Q, R, S इस प्रकार है कि, AP = BQ = CR = DS तो सिद्ध कीजिए कि `square` PQRS समांतर चतुर्भुज है।

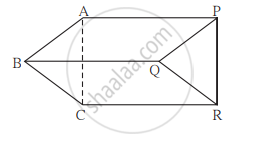
संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR