Advertisements
Advertisements
Question
नीचे दिये गये एक जहाज कौँ आकृति में, ABDH और CEFG दो समांतर चतुर्भुज हैं। x का मान ज्ञात कीजिए।
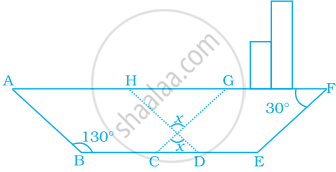
Solution
हमारे पास, समांतर चतुर्भुज ABDH और CEFG है।
अब, ABDH में,
∴ ∠ABD = ∠AHD = 130° ...[∵ समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।]
और ∠GHD = 180° – ∠AHD
= 180° – 130° ...[रैखिक युग्म]
⇒ ∠GHO = 50°
साथ ही, ∠EFG + ∠FGC = 180° ...[∵ समांतर चतुर्भुज के आसन्न कोण संपूरक होते हैं।]
⇒ 30° + ∠FGC = 180°
⇒ ∠FGC = 180° – 30° = 150°
और ∠HGC + ∠FGC = 180° ...[रैखिक युग्म]
∠HGC = 180° – ∠FGC
= 180° – 150°
∴ ∠HGO = 30°
ΔHGO में, कोण योग गुण का उपयोग करके,
∠OHG + ∠HGO + ∠HOG = 180°
⇒ 50° + 30° + x = 180°
⇒ x = 180° – 80°
= 100°
APPEARS IN
RELATED QUESTIONS
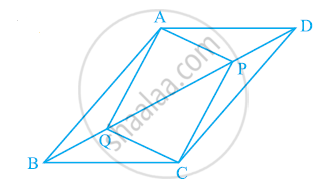
समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP = BQ है (देखिए आकृति में)। दर्शाइए कि
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ एक समांतर चतुर्भुज है।
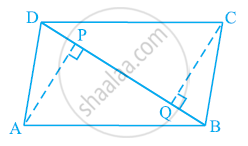
ABCD एक समांतर चतुर्भज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं (देखिए आकृति में)। दर्शाइए कि
- ΔAPB ≅ ΔCQD
- AP = CQ
निम्न समांतर चतुर्भुज में अज्ञात x,y,z के मानों को ज्ञात कीजिए:

निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:

क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि AB = DC = 8 cm, AD = 4 cm और BC = 4.4 cm?
किसी समांतर चतुर्भुज के दो आसन्न कोणों का अनुपात 3 : 2 है। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
दी गई आकृति में RISK तथा CLUE दोनों समांतर चतुर्भुज हैं, x का मान ज्ञात कीजिए।
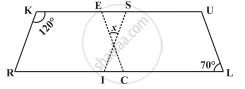
निम्नलिखित के लिए कारण दीजिए:
वर्ग एक समांतर चतुर्भुज भी है।
चतुर्भुज ABCD में, ∠A + ∠D = 180° है। इस चतुर्भुज को कौन-सा विशेष नाम दिया जा सकता है?
ABCD एक समचतुर्भुज है, जिसमें D से AB पर शीर्षलंब AB को समद्विभाजित करता है। समचतुर्भुज के कोण ज्ञात कीजिए।
यदि किसी समांतर चतुर्भुज के दो आसन्न कोण (5x − 5)∘ और (10x + 35)∘ हैं, तो इन कोणों का अनुपात होगा –
एक समांतर चतुर्भुज की आसन्न भुजाएँ 5 cm और 9 cm है। उसका परिमाप ______ है।
किसी चतुर्भुज के विकर्णों का प्रतिच्छेद बिंदु इनमें से एक को 1: 2 के अनुपात में विभाजित करता है। क्या यह एक समांतर चतुर्भुज होगा? क्यों और क्यों नहीं?
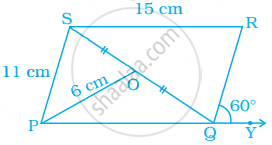
नीचे दिये समांतर चतुर्भुज PQRS में, O विकर्ण SQ का मध्य बिंदु है। ∠S, ∠R, PQ, QR और विकर्ण PR ज्ञात कीजिए।
किसी चतुर्भुज के दो कोणों में से प्रत्येक की माप 75∘ है तथा अन्य दो कोण बराबर हैं। इन दोनों कोणों के माप क्या हैं? संभावित बनने वाली आकृतियों के नाम लिखिए।
ABCD एक समांतर चतुर्भुज है। भुजा AB और AD पर क्रमशः बिंदु P और Q इस प्रकार लिये गये हैं कि एक समांतर चतुर्भुज PRQA बनता है। यदि ∠C = 45∘ है, तो ∠R ज्ञात कीजिए।
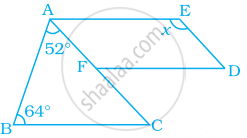
निम्न आकृति में, FD || BC || AE है और AC || ED है। x का मान ज्ञात कीजिए –
एक समांतर चतुर्भुज की रचना कीजिए जिसकी एक भुजा 4 cm और दोनों विकर्ण 5.6 cm और 7 cm हों। दूसरी भुजा को मापिए।
सिद्ध कीजिए कि एक समांतर चतुर्भुज के कोणों के समद्विभाजकों द्वारा बना चतुर्भुज एक आयत होता है।
