Advertisements
Advertisements
Question
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हो और परस्पर समद्विभाजित करें, तो वह एक वर्ग होता है |
Solution
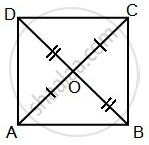
दिया है : ABCD एकचतुर्भुज है जिसमें विकर्ण AC = BD है और एक
दुसरे को बिंदु O पर प्रतिच्छेद करते है जहाँ AO = CO तथा BO = DO है
सिद्ध करना है : ABCD एक वर्ग है |
प्रमाण : ΔAOB तथा ΔCOD में
AO = CO (दिया है)
BO = DO (दिया है)
∠AOB = ∠COD (शिर्षाभिमुख कोण)
अत: SAS सर्वांगसमता नियम से
ΔAOB ≅ ΔCOD
∴ AB = CD (By CPCT) …… (1)
तथा ∠BAO = ∠DCO (एकांतर कोण) (By CPCT)
∴ AB || CD ......... (2) (एकांतर कोण बराबर हो तो रेखाएँ समांतर होती है )
समीo (1) तथा (2) से
ABCD एक समांतर चतुर्भुज है |
(यदि किसी चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर एवं समान्तर हो तो वह समान्तर चतुर्भुज होता है)
∴ AD = BC ........... (3) (समांतर चतुर्भुज की सम्मुख भुजा बराबर होती है)
अब ΔAOD तथा ΔCOD में
AO = CO (दिया है)
DO = DO (उभयनिष्ठ)
∠AOD = ∠COD (90o प्रत्येक)
अत: SAS सर्वांगसमता नियम से
ΔAOD ≅ ΔCOD
∴ AD = CD (By CPCT) …… (4)
समीo (1), (3) तथा (4) से हम पाते हैं |
AB = BC = CD = AD ........... (5)
अब, ΔABD तथा ΔABC में
AD = BC (वर्ग की सम्मुख भुजा)
AB = AB (उभयनिष्ठ)
BD = AC (दिया है)
SSS सर्वांगसमता नियम से
ΔABD ≅ ΔABD
∴ ∠A = ∠B (By CPCT) …… (6)
चूँकि ABCD एक वर्ग है |
∴ AD || BC और AB एक तिर्यक रेखा है |
अत: ∠A + ∠B = 180o (अंत: आसन्न कोणों का योग)
⇒∠A + ∠A = 180o ..समीo (6) से
⇒2∠A = 180o
⇒ ∠A = `180^circ/2 = 90^circ`
⇒∠A = 90o .......... (7)
समीo (5) तथा (7) से स्पष्ट है कि
ABCD एक वर्ग है
APPEARS IN
RELATED QUESTIONS
ABCD एक समचतुर्भुज है दर्शाइए कि AC कोणों A और C दोनों को समद्विभाजित करता है तथा विकर्ण BD कोणों B तथा D दोनों को समद्विभाजित करता है |
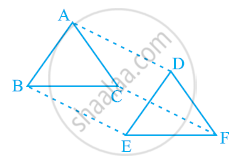
ΔABC और ΔDEF में, AB = DE, AB || DE, BC = EF और BC || EF है | शीर्षों A, B और C को क्रमश: शीर्षों D, E और F से जोड़ा जाता है | दर्शाइए कि
- चतुर्भुज ABED एक समांतर चतुर्भुज है।
- चतुर्भुज BEFC एक समांतर चतुर्भुज है।
- AD || CF और AD = CF है |
- चतुर्भुज ACFD एक समांतर चतुर्भुज है।
- AC = DF है
- Δ ABC ≅ Δ DEF है