Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram in which AE is perpendicular to CD as shown in the given figure. Also, AC = 5 cm, DE = 4 cm and area of ΔAED = 6 cm2. Find the perimeter and area of parallelogram ABCD.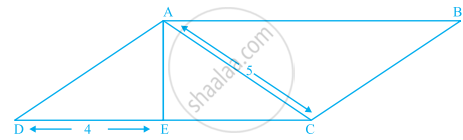
उत्तर
Given area of ΔAED = 6 cm2 and AC = 5 cm and DE = 4 cm
∴ Area of ΔAED = `1/2` × DE × AE ......[∵ Area of triangle = Base × Height]
⇒ `1/2` × 4 × AE = 6
⇒ AE = `(6 xx 2)/4`
⇒ AE = 3 cm
Now, In right-angled ΔAEC, AE = 3 cm and AC = 5 cm
So, = (EC)2 = (AC)2 – (AE)2 ......[By Pythagoras theorem]
⇒ (EC)2 = 52 – 32 = 25 – 9
⇒ EC = `sqrt(16)`
⇒ EC = 4 cm
∵ DE + EC = DC
⇒ DC = 4 + 4 = 8 cm
∵ ABCD is a parallelogram
So, AB = DC = 8 cm
Now, In right-angled ΔAED, AD2 = AE2 + ED2 ......[By Pythagoras theorem]
⇒ AD2 = 32 + 42 = 9 + 16
⇒ AD = `sqrt(25)`
⇒ AD = 5 cm
So, AD = BC = 5 cm ......[∵ ABCD is a parallelogram]
∴ Perimeter of paralielogram ABCD = 2(l + b) = 2(DC + AD) = 2(8 + 5) = 2 × 13 = 26 cm
Area of parallelogram ABCD = Base × Height = DC × AE = 8 × 3 = 24 cm.
APPEARS IN
संबंधित प्रश्न
PQRS is a parallelogram (see the given figure). QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:
- the area of the parallelogram PQRS
- QN, if PS = 8 cm

If base of a parallelogram is 18 cm and its height is 11 cm, find its area.
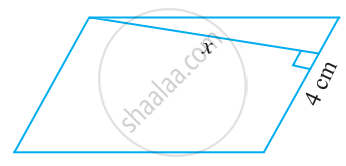
Find the height ‘x’ if the area of the parallelogram is 24 cm2 and the base is 4 cm.
Find the missing values.
| Base | Height | Area |
| 18 cm | 5 cm |
Find the missing values.
| Base | Height | Area |
| 8 cm | 56 sq.m |
The height of the parallelogram is one-fourth of its base. If the area of the parallelogram is 676 sq.cm, find the height and the base
If the base and height of a parallelogram are in the ratio 7 : 3 and the height is 45 cm, then fixed the area of the parallelogram
Find the height of the parallelogram whose base is four times the height and whose area is 576 sq.cm
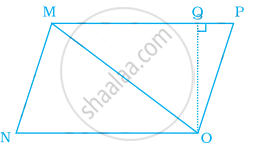
Ratio of area of ∆MNO to the area of parallelogram MNOP in the same figure is ______.
If the sides of a parallelogram are increased to twice its original lengths, how much will the perimeter of the new parallelogram?
