Question

Adjacent sides of a parallelogram are equal and one of the diagonals is equal to any one of the sides of this parallelogram. Show that its diagonals are in ratio √3:1.

Answer 1

If adjacent sides of a parallelogram are equal, then it is a rhombus.
Now, the diagonals of a rhombus bisect each other and are perpendicular to each other.
Let the lengths of the diagonals be x and y.
Diagonal of length y be equal to the sides of the rhombus.
Thus, each side of rhombus = y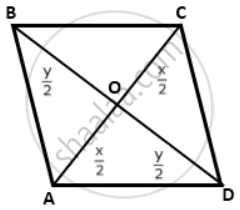

Now, in right-angles ΔBOC, by Pythagoras theorem
OB² + OC² = BC²
⇒ `(y/2)^2 + (x/2)^2 = y^2`

⇒ `(x^2/4) = y^2 - y^2/4`

⇒ `(x^2/4) = [ 4y^2 - y^2 ]/4`

⇒ `(x^2/4) = (3y^2)/4`

⇒ `x^2 = 3y^2`

⇒ `x^2/y^2 = 3/1`

⇒ `x/y = sqrt3/1`

Thus, the diagonal are in the ratio `sqrt3 : 1`