Advertisements
Advertisements
Question
Adjacent sides of a parallelogram are equal and one of the diagonals is equal to any one of the sides of this parallelogram. Show that its diagonals are in ratio √3:1.
Solution
If adjacent sides of a parallelogram are equal, then it is a rhombus.
Now, the diagonals of a rhombus bisect each other and are perpendicular to each other.
Let the lengths of the diagonals be x and y.
Diagonal of length y be equal to the sides of the rhombus.
Thus, each side of rhombus = y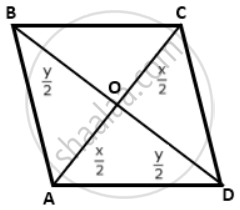
Now, in right-angles ΔBOC, by Pythagoras theorem
OB2 + OC2 = BC2
⇒ `(y/2)^2 + (x/2)^2 = y^2`
⇒ `(x^2/4) = y^2 - y^2/4`
⇒ `(x^2/4) = [ 4y^2 - y^2 ]/4`
⇒ `(x^2/4) = (3y^2)/4`
⇒ `x^2 = 3y^2`
⇒ `x^2/y^2 = 3/1`
⇒ `x/y = sqrt3/1`
Thus, the diagonal are in the ratio `sqrt3 : 1`
APPEARS IN
RELATED QUESTIONS
M and N divide the side AB of ΔABC into three equal parts. Line segments MP and NQ are both parallel to BC, and meet AC in P and Q respectively. Prove that P and Q divide AC into three equal parts.
In the given figure, the lines l, m and n are parallel to each other. D is the midpoint of CE. Find: a. BC, b. EF, c. CG and d. BD.
