Advertisements
Advertisements
प्रश्न
An electron in a hydrogen atom makes transitions from orbits of higher energies to orbits of lower energies.
- When will such transitions result in (a) Lyman (b) Balmer series?
- Find the ratio of the longest wavelength in the Lyman series to the shortest wavelength in the Balmer series.
उत्तर
(i) Emission spectrum of Hydrogen atom: Lyman and Balmer series
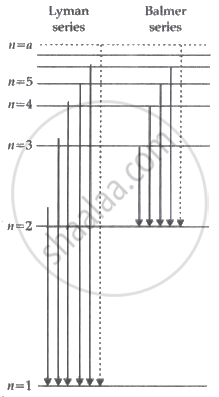
- Lyman Series: When electrons will jump from a higher energy orbit to n = 1 orbit.
- Balmer Series: When electrons will jump from a higher energy orbit yo n = 2 orbits.
(ii) Longest wavelength of Lyman series:
`1/λ_"L" = "R"_"H"[1/1^2 - 1/2^2] = "R"_"H" [3/4]`
Shortest wavelength of Balmer series:
`1/λ_"B" = "R"_"H"[1/2^2 - 1/(∞^2)] = "R"_"H" [1/4]`
Now,
`λ_"L"/λ_"B" = [4/3]/[4/1] = 1/3`
APPEARS IN
संबंधित प्रश्न
When is Hα line in the emission spectrum of hydrogen atom obtained? Calculate the frequency of the photon emitted during this transition.
Calculate the minimum wavelength of the spectral line present in Balmer series of hydrogen
Using Rydberg formula, calculate the longest wavelength belonging to Lyman and Balmer series. In which region of hydrogen spectrum do these transitions lie?
[Given R = 1.1 ✕ 107 m−1]
Using Rydberg formula, calculate the wavelengths of the spectral lines of the first member of the Lyman series and of the Balmer series.
The ground state energy of hydrogen atom is −13.6 eV. If and electron make a transition from the energy level −0.85 eV to −3.4 eV, calculate spectrum does his wavelength belong?
The ground state energy of hydrogen atom is −13.6 eV. If an electron make a transition from an energy level −0.85 eV to −1.51 eV, calculate the wavelength of the spectral line emitted. To which series of hydrogen spectrum does this wavelength belong?
A spectroscopic instrument can resolve two nearby wavelengths λ and λ + Δλ if λ/Δλ is smaller than 8000. This is used to study the spectral lines of the Balmer series of hydrogen. Approximately how many lines will be resolved by the instrument?
Hydrogen spectrum consists of discrete bright lines in a dark background and it is specifically known as hydrogen emission spectrum. There is one more type of hydrogen spectrum that exists where we get dark lines on the bright background, it is known as the absorption spectrum. Balmer found an empirical formula by the observation of a small part of this spectrum and it is represented by
`1/lambda = "R"(1/2^2 - 1/"n"^2)`, where n = 3, 4, 5,....
For Lyman series, the emission is from first state to nth state, for Paschen series, it is from third state to nth state, for Brackett series, it is from fourth state to nth state and for P fund series, it is from fifth state to nth state.
Which series of hydrogen spectrum corresponds to ultraviolet region?
Hydrogen spectrum consists of discrete bright lines in a dark background and it is specifically known as hydrogen emission spectrum. There is one more type of hydrogen spectrum that exists where we get dark lines on the bright background, it is known as absorption spectrum. Balmer found an empirical formula by the observation of a small part of this spectrum and it is represented by
`1/lambda = "R"(1/2^2 - 1/"n"^2)`, where n = 3, 4, 5,....
For Lyman series, the emission is from first state to nth state, for Paschen series, it is from third state to nth state, for Brackett series, it is from fourth state to nth state and for P fund series, it is from fifth state to nth state.
Which of the following lines of the H-atom spectrum belongs to the Balmer series?
Name the series of lines of hydrogen spectrum which lie in the visible region.
